
Galassia a spirale M81. Credito:NASA/JPL-Caltech/ESA/Harvard-Smithsonian CfA
L'astronomo del XVII secolo Johannes Kepler fu il primo a riflettere sulla struttura dei fiocchi di neve. Perché sono così simmetrici? Come fa una parte a sapere per quanto tempo è cresciuta la parte opposta? Keplero pensava che dipendesse tutto da quello che ora chiameremmo un "campo morfogenico" - che le cose volere avere la forma che hanno. Da allora la scienza ha scartato questa idea. Ma la domanda sul perché i fiocchi di neve e strutture simili siano così simmetrici non è ancora del tutto compresa.
La scienza moderna mostra quanto sia fondamentale la domanda:guarda tutte le galassie a spirale là fuori. Possono avere un diametro di mezzo milione di anni luce, ma conservano ancora la loro simmetria. Come? Nel nostro nuovo studio, pubblicato in Rapporti scientifici , presentiamo una spiegazione.
Abbiamo mostrato che informazione ed "entropia" - una misura del disordine di un sistema - sono collegate tra loro ("info-entropia") in un modo esattamente analogo ai campi elettrici e magnetici ("elettromagnetismo"). Le correnti elettriche producono campi magnetici, mentre i campi magnetici variabili producono correnti elettriche. L'informazione e l'entropia si influenzano a vicenda allo stesso modo.
L'entropia è un concetto fondamentale in fisica. Per esempio, perché l'entropia non può mai diminuire (il disordine aumenta sempre) puoi trasformare un uovo in uova strapazzate ma non viceversa. Se sposti le informazioni, devi anche aumentare l'entropia:una telefonata ha un costo di entropia.
Abbiamo mostrato che l'entropia e l'informazione possono essere trattate come un campo e che sono legate alla geometria. Pensa ai due filamenti della doppia elica del DNA che si avvolgono l'uno attorno all'altro. Le onde luminose hanno la stessa struttura, dove i due filamenti sono i campi elettrico e magnetico. Abbiamo dimostrato matematicamente che la relazione tra informazione ed entropia può essere visualizzata utilizzando la stessa geometria.

Un vero fiocco di neve. Credito:Karen Schanely:https://www.clickinmoms.com/blog/take-macro-snowflakes-pictures/; dominio pubblico
Volevamo vedere se la nostra teoria poteva prevedere le cose nel mondo reale, e ho deciso di provare a calcolare quanta energia avresti bisogno per convertire una forma di DNA in un'altra. Il DNA è dopo tutto una spirale e una forma di informazione.
Questo è stato effettivamente fatto con misurazioni straordinariamente precise circa 16 anni fa. I ricercatori hanno tirato dritto una molecola di DNA (al DNA piace rannicchiarsi), e l'ho attorcigliato 4, 800 giri tenendo le estremità con una pinzetta ottica. Il DNA è passato da una forma all'altra, come nella foto sopra. I ricercatori hanno quindi potuto calcolare la differenza di energia tra le due forme.
Ma la nostra teoria potrebbe calcolare questa differenza di energia, pure. Conoscevamo l'entropia di ciascuna delle due versioni di questa molecola di DNA, e l'energia è semplicemente il prodotto di entropia e temperatura. Il nostro risultato era esatto:la teoria sembrava reggere.
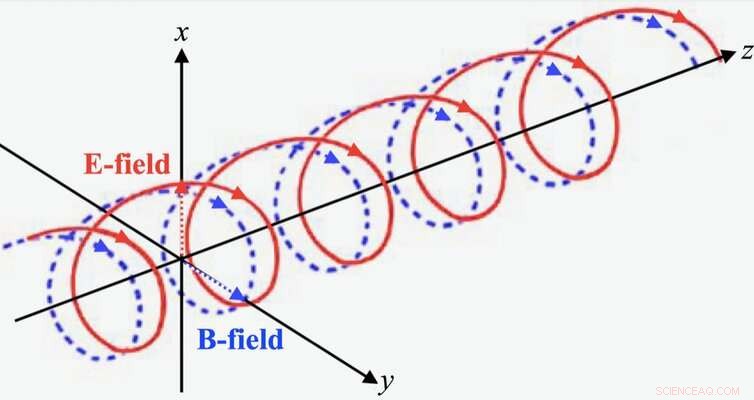
Onda luminosa con campi elettrici (E) e magnetici (B). Autore fornito
Da piccolo a enorme
Le galassie a spirale sono doppie spirali proprio come il DNA è una doppia elica:matematicamente parlando hanno geometrie simili.
La nostra teoria mostra direttamente perché i due bracci delle galassie a spirale sono simmetrici:è perché i campi di info-entropia danno origine a forze (come altri campi). Le stelle nella galassia sono semplicemente coreografate da una forza entropica per allinearsi in una coppia di tali spirali per massimizzare l'entropia.
Ma volevamo ottenere dei numeri reali, pure. Abbiamo quindi deciso di provare a calcolare la massa della nostra galassia dalla nostra teoria. Sappiamo quanto sembra essere pesante la Via Lattea dalla velocità con cui le stelle si muovono vicino al bordo galattico:si tratta di circa 1,3 trilioni di masse solari.
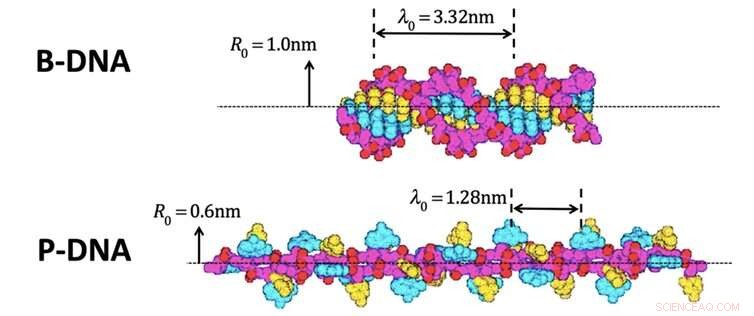
Due forme di DNA. Credito:Parker &Jeynes, Fig.1 dei Rapporti Scientifici 9|10779 (2019); Modificato dalla Fig. 5 di Allemand et al. Proc. Natl. Acad. Sci. Stati Uniti 95, 14152–14157 (1998), CC BY
Stranamente, questo è in realtà molto più della massa di tutte le stelle visibili nella galassia. Per essere in grado di spiegare questa discrepanza e spiegare perché le stelle si muovono molto più velocemente del previsto, gli astronomi hanno avuto l'idea della "materia oscura" - massa invisibile in agguato nella galassia, aumentando la sua attrazione gravitazionale sulle stelle.
Avevamo bisogno di conoscere l'entropia della galassia per i nostri calcoli. Per fortuna, il fisico matematico Roger Penrose ha mostrato che questa entropia è dominata dall'entropia del suo buco nero supermassiccio centrale.
Conosciamo la massa di questo buco nero (4,3 milioni di masse solari). E sorprendentemente, quando conosci la massa di un buco nero, c'è un'equazione scoperto dal defunto fisico Stephen Hawking, che ne calcola l'entropia. Hawking ha anche scoperto come calcolare la "temperatura" alla sua superficie, o "orizzonte degli eventi".
Se puoi assegnare una "temperatura" all'orizzonte degli eventi del buco nero, che non contiene elementi per avere la temperatura, perché non assegnare una temperatura anche a una galassia? Nel nostro articolo sosteniamo che ciò è ragionevole (usando il cosiddetto "principio olografico"). Quindi abbiamo usato le nostre equazioni di info-entropia per calcolare la temperatura olografica della galassia.

Una galassia a spirale con una spirale logaritmica a doppio braccio sovrapposta. Credito:Parker &Jeynes, Fig.2 di Rapporti scientifici 9|10779 (2019), CC BY-SA
Allora diventa facile. Sappiamo che l'energia galattica è data dal prodotto della sua entropia e temperatura. E quando conosciamo l'energia possiamo scoprire la massa grazie alla famosa equazione di Einstein:E=mc 2 .
Questa volta il risultato non è stato proprio azzeccato, ma era ragionevolmente vicino dato il nostro modello altamente semplificato della galassia. La geometria info-entropica di una galassia non solo spiega come le forze entropiche creano la forma meravigliosamente simmetrica e la mantengono, ma spiega anche tutta la massa che in essa appare evidente.
Ciò significa che in realtà non abbiamo bisogno della materia oscura, dopotutto. Secondo il nostro modello, l'entropia galattica dà origine a una quantità così grande di energia aggiuntiva che modifica la dinamica osservata della galassia, facendo muovere le stelle ai margini più velocemente del previsto. Questo è esattamente ciò che la materia oscura avrebbe dovuto spiegare. L'energia non è direttamente osservabile come massa, ma la sua presenza è certamente supportata dalle osservazioni astronomiche, che spiegano perché le ricerche sulla materia oscura finora non hanno trovato nulla.
Tuttavia, ci sono molte ricerche a sostegno dell'idea della materia oscura. La nostra teoria suggerisce una spiegazione alternativa delle osservazioni, e non ha bisogno di nuova fisica. Certo, è necessario un lavoro più dettagliato per verificare che anche la reale complessità delle osservazioni possa essere modellata con successo.
Pensiamo che il "campo morfogenico" che Keplero stava cercando esista davvero, ed è in realtà l'effetto dell'intreccio di informazione ed entropia. Dopo quattro lunghi secoli, sembra che Keplero sia stato finalmente vendicato.
Questo articolo è stato ripubblicato da The Conversation con una licenza Creative Commons. Leggi l'articolo originale. 