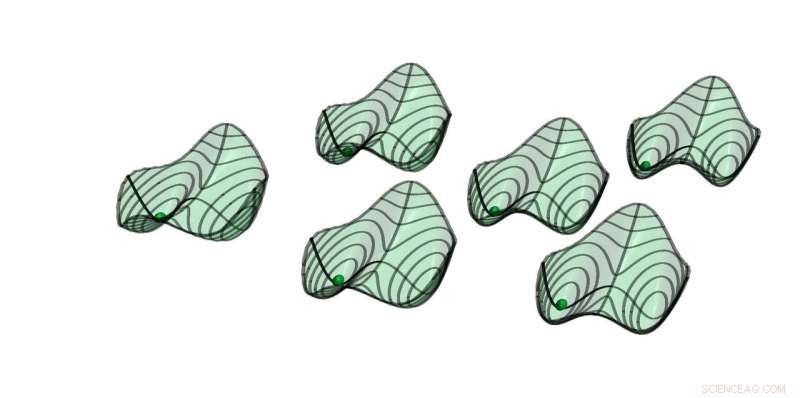
Quasi potenziali di sei oscillatori parametrici con accoppiamento debole all-to-all. Le soluzioni stabili si trovano ai minimi. Le palline indicano la soluzione simmetrica, dove tutti gli oscillatori sono in fase. (Screenshot dall'animazione di accompagnamento) Credito:ETH Zurigo/D-PHYS Toni Heugel
Strutture note come cristalli temporali, che si ripetono nel tempo come i cristalli convenzionali si ripetono nello spazio, hanno recentemente catturato l'interesse e l'immaginazione dei ricercatori di tutte le discipline. Il concetto è emerso dal contesto dei sistemi quantistici a molti corpi, ma i fisici dell'ETH hanno ora sviluppato un quadro versatile che chiarisce i collegamenti con le opere classiche risalenti a quasi due secoli fa, fornendo così una piattaforma unificante per esplorare fenomeni apparentemente dissimili.
In un cristallo, gli atomi sono altamente ordinati, occupando posizioni ben definite che formano modelli spaziali. Sette anni fa, il premio Nobel per la fisica del 2004 Frank Wilczek ha valutato la possibilità di un analogo temporale dell'ordine spaziale cristallino:sistemi che mostrano modulazioni temporali periodiche sostenute nel loro stato di energia più bassa. Il concetto di tali strutture con uno stato fondamentale oscillante è molto intrigante. ahimè, non molto tempo dopo la pubblicazione dell'idea, è stato dimostrato che tali cristalli temporali non sono possibili senza infrangere le leggi fondamentali della fisica. Però, successivi lavori teorici hanno suggerito che quando i sistemi quantistici a molti corpi sono periodicamente guidati, emergono nuove correlazioni temporali persistenti che evocano i cristalli temporali di Wilczek. Questi sistemi guidati sono stati soprannominati cristalli temporali discreti, e nel 2017, le prime realizzazioni sperimentali di tali stati sono state riportate in insiemi di particelle accoppiate (ioni, elettroni e nuclei) che mostrano proprietà quantomeccaniche.
Una storia non così breve dei cristalli del tempo
In poco tempo, osservatori astuti hanno individuato somiglianze distinte tra i cristalli a tempo discreto nei sistemi quantistici e i cosiddetti risonatori parametrici, un concetto nella fisica classica che risale al lavoro di Michael Faraday nel 1831. La connessione tra questi due corpi di lavoro è rimasta, però, opaco. Ora, i teorici hanno sviluppato una nuova struttura che fa molto per sollevare le ambiguità che circondano le somiglianze tra i sistemi classici e quantistici periodicamente guidati.
Scrivendo in un articolo pubblicato oggi sulla rivista Lettere di revisione fisica , Toni Heugel, un dottorato di ricerca studente presso il Dipartimento di Fisica dell'ETH di Zurigo, e Matthias Oscity, uno studente presso la stessa istituzione, lavorando con il Dr. Ramasubramanian Chitra e il Prof. Oded Zilberberg dell'Istituto di Fisica Teorica e con il Dr. Alexander Eichler del Laboratorio di Fisica dello Stato Solido, riportare un lavoro teorico e sperimentale che stabilisca come possono essere generati cristalli a tempo discreto che, da una parte, non richiedono effetti meccanici quantistici e, d'altra parte, mostrare effetti a molti corpi genuini, che è una caratteristica dei cristalli a tempo discreto riportati nei sistemi quantistici.
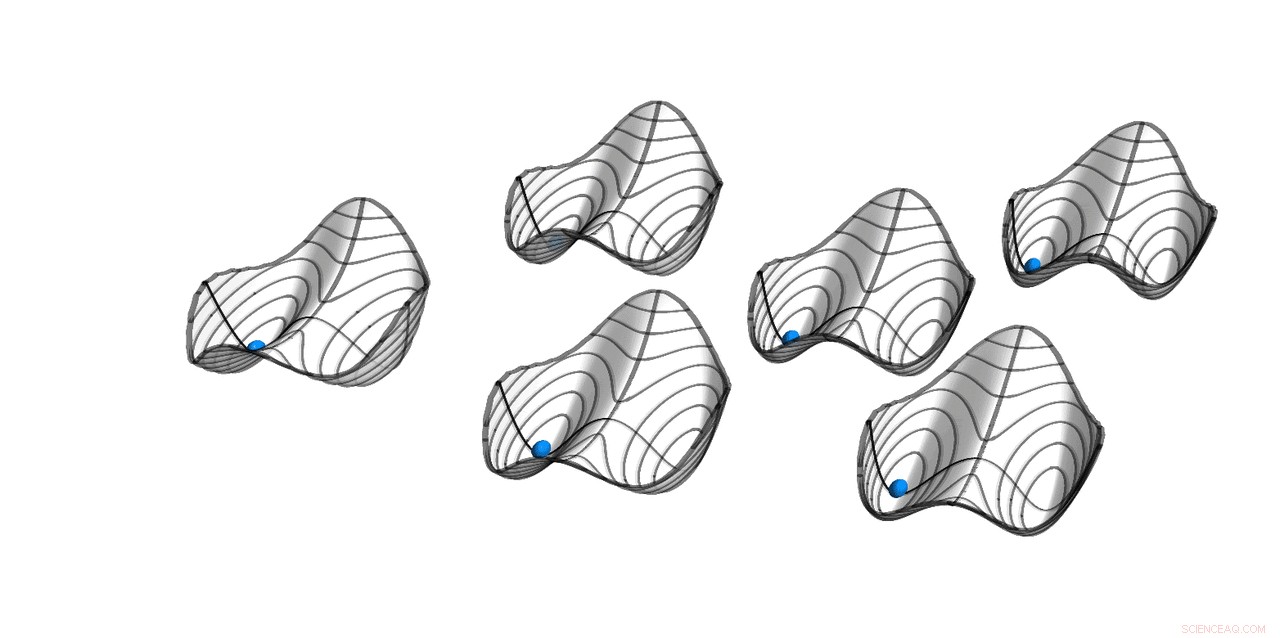
Quasi potenziali di sei oscillatori parametrici con accoppiamento debole all-to-all. Le soluzioni stabili si trovano ai minimi. Le palline indicano la soluzione simmetrica, dove tutti gli oscillatori sono in fase. L'Hamiltoniana H governa il moto del sistema di periodo T, mentre la soluzione stessa ha periodo 2T. Questa rottura della simmetria di traslazione temporale discreta rende il sistema un cristallo temporale discreto. Credito:ETH Zurigo/D-PHYS Toni Heugel
Molti modi per frequenze subarmoniche
C'è un'ovvia somiglianza tra i classici risonatori parametrici e i cristalli a tempo discreto realizzati sperimentalmente nei sistemi quantistici a molti corpi:entrambi mostrano dinamiche emergenti a frequenze che sono frazioni della frequenza di guida. Nel contesto dei cristalli a tempo discreto, l'emergere di oscillazioni a tali frequenze subarmoniche rompe la periodicità temporale del sistema guidato, fornendo un "analogo temporale" all'ordine spaziale cristallino, in cui la simmetria dello spazio è rotta. Nei classici sistemi guidati parametricamente, le frequenze subarmoniche appaiono in modi più familiari:un bambino su un'altalena, ad esempio, modifica il baricentro al doppio della frequenza dell'oscillazione risultante, o la coda di cavallo di un corridore oscilla alla metà della frequenza del movimento verticale della testa.
Ma questi fenomeni dissimili hanno qualcosa a che fare l'uno con l'altro? Sì, dicono i fisici dell'ETH. In particolare, essi individuano dove appaiono gli aspetti a molti corpi nei sistemi classici. Fare così, hanno considerato oscillatori non lineari classici con accoppiamento sintonizzabile tra di loro.
Quadro unificante per sistemi classici e quantistici guidati periodicamente
È risaputo che per determinate frequenze e intensità di pilotaggio, gli oscillatori parametrici diventano instabili e quindi subiscono una cosiddetta biforcazione di raddoppio del periodo, oltre la quale oscillano a metà della loro frequenza di pilotaggio. Heugel, Oscity e i loro colleghi esplorano cosa succede quando molti di questi oscillatori vengono accoppiati insieme. Nei calcoli e negli esperimenti utilizzando due stringhe con accoppiamento variabile tra loro, trovano due regimi distinti. Quando l'accoppiamento è forte, il sistema a due corde si muove collettivamente, ricreando in sostanza i movimenti del bambino su un'altalena o la coda di cavallo di un corridore. Però, in caso di accoppiamento debole tra le corde, le dinamiche di ogni stringa sono simili a quelle visualizzate dal sistema disaccoppiato. Come conseguenza, gli oscillatori accoppiati non si biforcano collettivamente ma si biforcano individualmente a parametri leggermente diversi dell'azionamento, portando a dinamiche complessive più ricche, che diventano sempre più complesse man mano che i sistemi si ingrandiscono.
I ricercatori dell'ETH sostengono che tali modalità debolmente accoppiate sono simili a quelle che emergono nei sistemi quantistici a molti corpi, implicando che la loro struttura potrebbe spiegare i comportamenti osservati sperimentalmente in questi sistemi. Inoltre, il nuovo lavoro prescrive le condizioni generali per la generazione di cristalli temporali classici a molti corpi. Questi potrebbero in definitiva essere usati sia per interpretare che per esplorare le caratteristiche delle loro controparti quantistiche.
Presi insieme, questi risultati forniscono quindi un potente quadro unificante per sistemi classici e quantistici guidati periodicamente che mostrano dinamiche a frequenze subarmoniche emergenti, sistemi che sono stati finora descritti in contesti molto diversi, ma potrebbe non essere poi così dissimile.