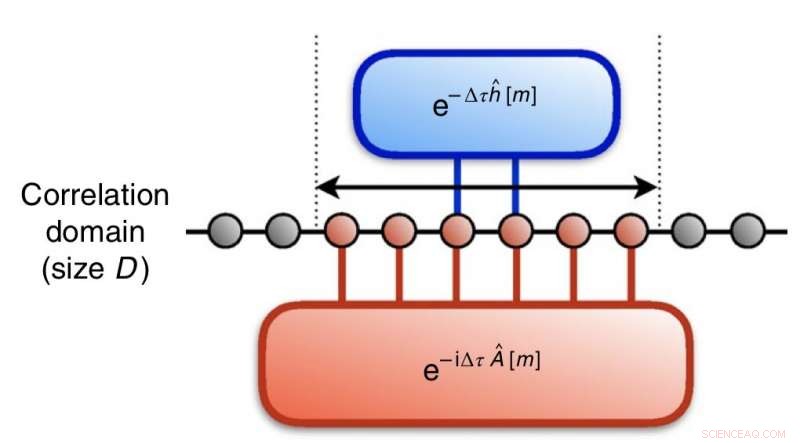
Immagine che cattura l'essenza di come i ricercatori hanno rappresentato l'evoluzione del tempo immaginario mediante trasformazioni unitarie che si possono trasformare in un circuito quantistico. Credito:Motta et al.
Determinare il comportamento quantomeccanico di molte particelle interagenti è essenziale per risolvere importanti problemi in una varietà di campi scientifici, compresa la fisica, chimica e matematica. Ad esempio, per descrivere la struttura elettronica di materiali e molecole, i ricercatori devono prima trovare il terreno, stati eccitati e termici dell'approssimazione hamiltoniana di Born-Oppenheimer. Nella chimica quantistica, l'approssimazione di Born-Oppenheimer è l'assunzione che i moti elettronici e nucleari nelle molecole possano essere separati.
Una varietà di altri problemi scientifici richiedono anche il calcolo accurato del suolo hamiltoniano, stati eccitati e termici su un computer quantistico. Un esempio importante sono i problemi di ottimizzazione combinatoria, che può essere ridotto alla ricerca dello stato fondamentale di opportuni sistemi di spin.
Finora, le tecniche per il calcolo degli autostati hamiltoniani su computer quantistici sono state principalmente basate sulla stima di fase o algoritmi variazionali, che sono progettati per approssimare l'autostato di energia più bassa (cioè, stato fondamentale) e un certo numero di stati eccitati. Sfortunatamente, queste tecniche possono presentare notevoli svantaggi, che li rendono impraticabili per risolvere molti problemi scientifici.
Una collaborazione di ricerca tra i gruppi di Garnet Chan, Fernando Brandao, e Austin Minnich del California Institute of Technology (Caltech) ha recentemente portato allo sviluppo di tre nuovi algoritmi che potrebbero aiutare a superare i limiti della stima di fase e dei metodi variazionali esistenti. Questi algoritmi, soprannominata evoluzione del tempo immaginario quantistico, Lanczos quantistico e algoritmi METTS quantistici, sono stati presentati in un articolo pubblicato in Fisica della natura .
"Terra determinante, stati eccitati e termici è ovviamente un problema importante nel calcolo quantistico, ma gli algoritmi per affrontarlo sull'hardware contemporaneo richiedono in genere importanti risorse quantistiche, come i circuiti quantistici profondi (cioè comprendenti molte porte quantistiche, e quindi incline alla decoerenza e all'implementazione imperfetta) e qubit ausiliari (cioè aggiuntivi) o ottimizzazioni dei parametri classici rumorosi non lineari, "Mario Motta, uno dei ricercatori che ha condotto lo studio, ha detto a Phys.org.
L'obiettivo principale del recente studio condotto dai ricercatori del Caltech era sviluppare nuovi algoritmi quantistici per determinare il terreno, stati eccitati e termici su computer quantistici. I ricercatori hanno cercato di aggirare i limiti pratici delle tecniche esistenti per il calcolo degli stati hamiltoniani sfruttando le nozioni della fisica informatica classica, come l'evoluzione del tempo immaginario, diagonalizzazione esatta e campionamento a temperatura finita, alla fine estendendo questi
nozioni agli algoritmi di calcolo quantistico al di là di quanto realizzato in precedenza.
"I nostri algoritmi si basano sulla nozione di evoluzione del tempo immaginario, che è simile a un processo di raffreddamento, " ha spiegato Motta. "Supponiamo di poter preparare un sistema quantomeccanico in un'approssimazione semplice ma imprecisa per lo stato fondamentale, una funzione d'onda di prova. Applicando questo processo di raffreddamento al sistema, possiamo rimuovere sistematicamente le eccitazioni spurie dalla funzione d'onda di prova, avvicinandosi così gradualmente allo stato fondamentale. Questo è il contenuto dell'algoritmo di evoluzione del tempo immaginario quantistico (QITE)."
I tre algoritmi sviluppati dai ricercatori del Caltech sono in qualche modo simili alle tecniche classiche per la ricerca di stati fondamentali ed eccitati. Raccogliendo informazioni mentre si svolge l'evoluzione del tempo immaginario, però, questi algoritmi possono formulare e risolvere un problema agli autovalori che fornisce l'accesso a stati eccitati specifici, impiegando una variante quantistica dell'approccio di Lanczos, una tecnica matematica ben consolidata per calcolare autovalori e autovettori.
"Certo, l'evoluzione del tempo immaginario può essere utilizzata anche per raffreddare un sistema da una temperatura infinita a una finita (maggiore di zero), e quindi per calcolare le proprietà a temperatura finita, come facciamo nel nostro algoritmo QMETTS, " ha detto Motta.
L'algoritmo di evoluzione del tempo immaginario quantistico e l'algoritmo di Lanczos proposti dai ricercatori presentano numerosi vantaggi rispetto alle tecniche esistenti e classiche. Ad esempio, poiché sono radicati nell'intuizione fisica, possono essere implementati su hardware quantistico contemporaneo e non richiedono circuiti profondi, qubit ausiliari e complicate ottimizzazioni dei parametri, indispensabili per altri algoritmi quantistici.
"Il risultato più significativo del nostro studio è stata la concezione di una suite di nuovi algoritmi per lo studio di sistemi a molti-molti-corpi sui computer quantistici contemporanei, " Ha detto Motta. "I nostri algoritmi portano utili spunti di riflessione nel campo della Fisica:in particolare, mostrano come la combinazione di idee e tecniche provenienti da diversi campi della scienza possa essere combinata sinergicamente per produrre tecniche innovative.''
Nel loro studio, Motta e i suoi colleghi hanno dimostrato l'efficacia degli algoritmi che hanno sviluppato implementandoli sulla macchina virtuale quantistica Rigetti e sull'unità di elaborazione quantistica Aspen-1. In queste dimostrazioni gli algoritmi si sono comportati molto bene, confrontando favorevolmente le tecniche esistenti per il calcolo del suolo hamiltoniano, stati eccitati e termici.
I nuovi algoritmi sviluppati da questo team di ricercatori potrebbero essere utilizzati in una varietà di studi che coinvolgono simulazioni quantistiche e ottimizzazione. Inoltre, potrebbero essere affinati ed estesi per soddisfare le esigenze dei singoli progetti di ricerca.
"La nostra ricerca futura sarà diretta ad espandere il potere predittivo degli algoritmi che abbiamo sviluppato, " Disse Motta. "Per esempio, calcolando proprietà oltre l'energia, come operatori di densità e funzioni di correlazione, e ideando strategie sistematiche ed efficienti per studiare sistemi arbitrari a molti corpi (comprendenti bosoni e fermioni, con particolare enfasi sulle molecole)."
© 2019 Scienza X Rete