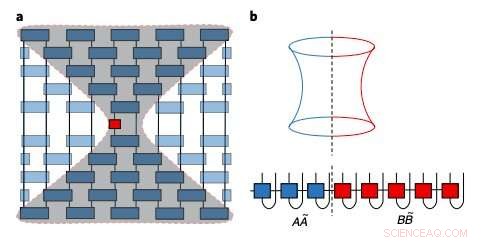
Schema del cono di luce emergente e della struttura di entanglement degli operatori di Heisenberg locali in forme di reti tensoriali. Credito:Xu &Swingle.
Nella fisica quantistica, lo scrambling è la dispersione delle informazioni quantistiche attraverso un sistema quantistico complesso, come i sistemi quantistici caotici a molti corpi. Questo processo può rendere difficile o impossibile l'accesso alle informazioni quantistiche, in particolare quando si utilizzano metodi fisici semplici e convenzionali.
Lo scrambling può essere misurato utilizzando correlatori out-of-time-ordered (OTOC), che sono misure del caos quantistico legate alla crescita degli operatori di Heisenberg. I ricercatori dell'Università del Maryland hanno recentemente introdotto un nuovo metodo per calcolare gli OTOC degli operatori locali nei sistemi 1-D. Questo metodo, presentato in un articolo pubblicato in Fisica della natura , potrebbe infine essere utilizzato per studiare lo scrambling in sistemi quantistici complessi.
"Il problema di base che stavamo cercando di capire è come il caos si diffonde nello spazio nei sistemi quantistici, "Brian Swing, uno dei ricercatori che ha condotto lo studio, ha detto a Phys.org. "Pensa all'esperimento mentale dell'effetto farfalla:volevamo sapere:se una farfalla sbatte le ali, quanto velocemente si diffonde quella perturbazione nello spazio? Volevamo capirlo specificamente nel contesto dei sistemi quantistici composti da molte particelle".
Precedenti studi su come il caos si diffonde nello spazio all'interno dei sistemi quantistici hanno raccolto diverse osservazioni interessanti, dipingendo un paesaggio interessante ma piuttosto complesso di possibili comportamenti. Molti di questi studi, però, si basavano su assunzioni speciali e questo rende più difficile determinare fino a che punto le loro conclusioni possono essere generalizzate ad altri sistemi.
Nel loro studio, Swingle e il suo collega Shenglong Xu hanno deciso di indagare quali comportamenti svelati in studi precedenti sono generici a tutti i sistemi quantistici. Speravano anche di capire come si può pensare al panorama delle possibilità che si verificano in diversi sistemi speciali.
"Per capire quale fosse il comportamento generico, avevamo bisogno di un metodo per calcolare gli OTOC nei sistemi generici, Swingle ha detto. "Un tale metodo dovrebbe utilizzare alcune proprietà generiche degli OTOC nei sistemi locali".
L'idea dei ricercatori era quella di utilizzare la proprietà del cono di luce dei sistemi quantistici, il che implica che al di fuori del cono di influenza in espansione derivante dal metaforico battito d'ala della farfalla, il sistema è poco perturbato. In altre parole, al di fuori del "cono della farfalla" l'effetto della farfalla rimane piccolo.
Nella meccanica quantistica, le azioni sono rappresentate come operatori e la piccolezza di un dato effetto si traduce nella semplicità dell'operatore. Facendo leva su questa semplicità, Swingle e Xu sono stati in grado di rappresentare l'operatore in un modo computazionalmente utile (cioè, come 'operatore di prodotti a matrice'), per eseguire i calcoli necessari per accedere allo scrambling.
"Ci sono due risultati chiave nel nostro studio, " Disse Swingle. "In primo luogo, abbiamo ideato un quadro teorico per classificare i vari possibili comportamenti dell'OTOC. Questo quadro era abbastanza generale da includere tutti gli esempi precedentemente noti. Secondo, abbiamo formulato un metodo di uso generale per calcolare gli OTOC, un metodo che potrebbe andare oltre i calcoli precedenti."
Swingle e Xu hanno già utilizzato il loro metodo per calcolare gli OTOC degli operatori locali per studiare una varietà di sistemi generici. interessante, hanno scoperto che molti di questi sistemi si adattano al loro quadro teorico. In uno studio di follow-up presentato in Revisione fisica X , i ricercatori hanno anche usato il loro metodo per raccogliere prove che gli OTOC nei sistemi caotici generici hanno un comportamento universale.
"Abbiamo proseguito questo lavoro applicando la nostra tecnologia a diversi sistemi studiati in esperimenti da tavolo in tutto il mondo, " Swingle ha detto. "Ora stiamo anche generalizzando l'approccio per includere nuovi tipi di effetti, compreso lo studio di sistemi a bassa temperatura dove la velocità di diffusione del caos tende a rallentare".
© 2019 Science X Network