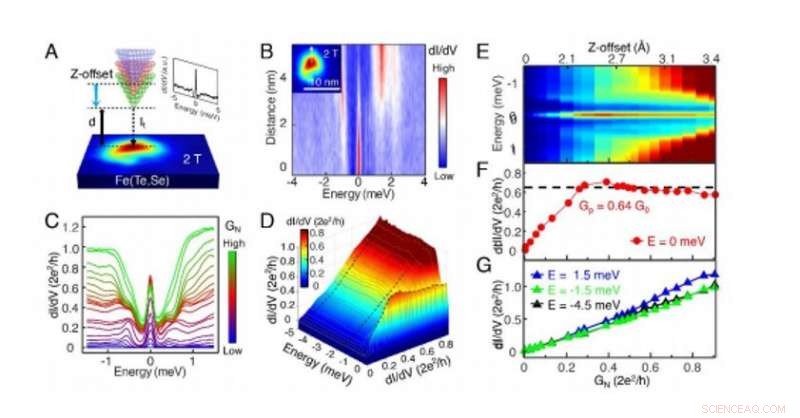
Plateau di conduttanza zero bias osservato su FeTe0.55Se0.45. (A) Uno schema del metodo STM/S di accoppiamento a tunnel variabile. Una mappa di conduttanza a polarizzazione zero sotto 2.0 T è mostrata su una superficie campione. Uno spettro dI/dV misurato al centro del nucleo del vortice (Vs=-5 mV, esso =500 pA, Vmod =0,02 mV) è mostrato nel riquadro in alto a destra, si osserva un picco di conduttanza a polarizzazione zero (ZBCP). Quando la corrente di tunneling (It) è regolata dall'anello di regolazione STM, l'accoppiamento del tunnel tra la punta STM e l'MZM può essere sintonizzato continuamente dalla distanza punta-campione (d). Un accoppiamento del tunnel più grande corrisponde a una conduttanza d minore e maggiore della barriera di tunneling (GN =It/Vs, Vs è la tensione di riferimento). L'offset Z può essere letto simultaneamente, che indica il movimento assoluto in direzione z della punta STM. (B) Un grafico dell'intensità del taglio di linea lungo la freccia bianca tratteggiata nel riquadro, misurato dallo stesso vortice mostrato in (A), mostrando un MZM stabile attraverso il nucleo del vortice. (C) Un grafico sovrapposto di spettri dI/dV sotto diversi valori di accoppiamento del tunnel parametrizzati in GN. La curva blu viene misurata sotto il GN più piccolo mentre la curva verde con il GN più grande. (D) Un grafico tridimensionale della misurazione dipendente dall'accoppiamento del tunnel, dI/dV(E, GN). Per chiarezza, solo i punti dati nell'intervallo di energia di [-5.0, 0.2] meV sono mostrati. (E) Un grafico in scala di colori di (C) all'interno dell'intervallo di energia di [-1,5, 1.5] meV che espande gli spettri in funzione di GN. Le informazioni sull'offset z, che è stato preso contemporaneamente da STM, è anche etichettato sull'asse superiore. La distanza massima raggiunta dalla punta è di 3,4 . (F) Un taglio di linea orizzontale allo zero bias da (E). La curva di conduttanza mostra un comportamento di plateau con la sua conduttanza di plateau (GP) pari a (0,64 ± 0,04) G0. (G) Linee orizzontali a valori di bias elevati da (E). L'assenza di un plateau di conduttanza su queste curve indica il comportamento di tunneling convenzionale all'energia degli stati continui. Tutti i dati sono misurati a Teff =377 mK. Credito: Scienza , doi:10.1126/science.aax0274
Quando un nanofilo semiconduttore è accoppiato a un superconduttore, può essere sintonizzato su stati quantistici topologici pensati per ospitare quasiparticelle localizzate note come Majorana Zero Modes (MZM). Gli MZM sono le loro antiparticelle, con applicazioni promettenti nel calcolo quantistico topologico. A causa dell'equivalenza particella-antiparticella, Gli MZM mostrano una conduttanza quantizzata a basse temperature. Sebbene esistano molte proposte teoriche per realizzare MZM in sistemi a stato solido, la loro realizzazione sperimentale si confronta con le non-idealità.
In un nuovo rapporto in Scienza , Shiyu Zhu e un team di ricercatori interdisciplinari in Cina e negli Stati Uniti hanno utilizzato la spettroscopia di tunneling a scansione accoppiata a tunnel variabile per studiare la conduttanza di tunneling degli stati legati al vortice dei superconduttori. Ad esempio, i superconduttori hanno un "gap" di energia in assenza di stati di elettroni, quindi gli elettroni non possono entrare in tunnel, mentre in una linea di vortice il campo magnetico chiuderà il divario per formare stati di elettroni. I ricercatori hanno riportato osservazioni con FeTe 0,55 Vedi 0.45 superconduttori, dove hanno registrato i plateau di conduttanza in funzione dell'accoppiamento tunneling per gli stati legati al vortice a energia zero, con valori vicini a, e anche raggiungendo, il valore di conduttanza quantistica universale 2e 2 /h; dove e, è la carica dell'elettrone e h è la costante di Planck. In contrasto, non hanno osservato altipiani né su stati legati al vortice di energia finita né all'interno del continuum di stati elettronici al di fuori del gap superconduttore. Questo comportamento della conduttanza in modalità zero ha supportato l'esistenza di MZM in FeTe 0,55 Vedi 0.45 cristalli .
I Modi Zero di Majorana (MZM) obbediscono a statistiche non abeliane, cioè eccitazioni oltre i soliti modi di eccitazione fermionici o bosonici, svolgere un ruolo estremamente importante nella computazione quantistica. Negli ultimi due decenni, i fisici hanno predetto MZM all'interno di superconduttori a onda p e materiali accoppiati spin-orbita vicini (per realizzare proprietà di un materiale assente da qualsiasi regione costituente dell'eterostruttura), da superconduttori ad onde s. I ricercatori avevano osservato prove sperimentali per MZM in vari sistemi, inclusi nanofili semiconduttori-superconduttori, eterostrutture topologiche isolante-superconduttore e catene atomiche su substrati superconduttori. Fisici e scienziati dei materiali hanno anche recentemente sviluppato superconduttori sfusi a base di ferro completamente gappati come piattaforma monomateriale per realizzare MZM. Successivamente, hanno trovato prove di MZM nei vortici topologici sulla superficie di FeTe 0,55 Vedi 0.45 cristalli mediante microscopia/spettroscopia a effetto tunnel a scansione (STM/S).
La conduttanza di un MZM può esibire un plateau quantizzato a temperature sufficientemente basse al valore di 2e 2 /h; dove e è la carica dell'elettrone e h la costante di Planck. Questa conduttanza di Majorana quantizzata risulta dalla perfetta riflessione risonante di Andreev, un tipo di dispersione di particelle che si verifica alle interfacce tra un superconduttore e un materiale allo stato normale, garantita dalla simmetria particella-foro intrinseca di MZM. Gli scienziati avevano osservato un plateau di conduttanza quantizzata in un sistema di nanofili InSb-Al, coerente con l'esistenza di MZM. Allo stesso modo, i superconduttori a base di ferro con picchi di conduttanza a polarizzazione zero (ZBCP) ottenuti utilizzando esperimenti STM/S hanno ampi gap topologici e offrono la possibilità di osservare la conduttanza quantizzata di Majorana, senza contaminazione da stati legati di Caroli-de Gennes-Matricon (CBS) a bassa quota. A seguito di precedenti prospettive sperimentali, Zhu et al. attualmente impiegato un metodo STM/S di accoppiamento tunnel variabile per studiare la conduttanza di Majorana attraverso un'ampia gamma di distanza punta-campione nei nuclei di vortice di FeTe 0,55 Vedi 0.45 campioni di cristallo.
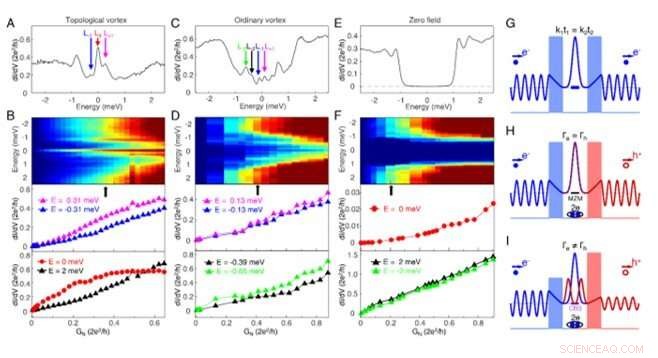
Risonanza indotta da Majorana Riflessione di Andreev. (A) Uno spettro dI/dV misurato al centro di un vortice topologico (Vs=-5mV, esso =140 nA, Vmod =0,02 mV), che mostra un MZM (freccia rossa) che coesiste con un CBS di alto livello situato a ± 0,31 meV. (B) Una misurazione dipendente dall'accoppiamento del tunnel sul vortice mostrato su (A) a 2 T. Pannello superiore:un grafico a scala di colori, dI/dv. La posizione GN di (A) è contrassegnata da una freccia nera. Pannello centrale:evoluzione dell'accoppiamento tunnel della conduttanza CBS, che non mostra alcun comportamento di plateau. Pannello inferiore:accoppiamento tunnel evoluzione della conduttanza alle energie di 0 meV (cerchi rossi, esibendo un plateau) e 2 meV (triangoli neri monotonicamente crescenti). (C) Uno spettro dl/dv misurato al centro di un vortice ordinario (Vs=-5mV, esso =140 nA, Vmod =0,02 mV), che mostra chiaramente tre livelli di CBS a ±0.13 meV (frecce magenta e blu), ±0.39 meV (frecce nere) e ±0.65 meV (freccia verde). (D) Simile a (B) ma misurato sul vortice mostrato in (C). Pannelli intermedi e inferiori:evoluzione dell'accoppiamento a tunnel della conduttanza CBS, non mostra alcuna caratteristica di plateau. (E) Uno spettro dI/dV misurato a 0T (Vs=-5mV, esso =80 nA, Vmod =0,02 mV). Si può vedere un gap superconduttore duro. (F) Simile a (B) e (D), ma misurata sotto 0 T. Pannello centrale:evoluzione dell'accoppiamento tunnel della conduttanza zero-bias (caso di giunzione normale metallo-superconduttore). Pannello inferiore:evoluzione dell'accoppiamento del tunnel all'energia del gap sopra (caso di giunzione metallo normale-metallo normale). Non c'è comportamento di plateau a 0 T. (G) Uno schema di tunneling risonante attraverso un sistema di barriera simmetrico. Viene mostrata l'evoluzione della funzione d'onda di un elettrone tunnellizzato. kt è la costante di penetrazione. (H) La vista a doppia barriera della riflessione Andreev risonante indotta da MZM. I colori blu e rosso indicano il processo di elettroni e lacune, rispettivamente. L'equivalenza delle componenti particella e lacuna in MZM garantisce lo stesso accoppiamento tunnel sulla barriera di elettroni e lacune. (I) La visione a doppia barriera della riflessione di Andreev mediata da una CBS. La miscelazione arbitraria di componenti particella-foro in CBS rompe la condizione di risonanza. Tutti i dati sono misurati a 377 mK. Credito: Scienza , doi:10.1126/science.aax0274
La temperatura effettiva degli elettroni del microscopio a effetto tunnel (STM) era di 377 mK e i ricercatori hanno sintonizzato continuamente l'accoppiamento del tunnel modificando la distanza punta-campione, che correla con la conduttanza tunnel-barriera. Applicando un campo magnetico di 2 T (Tesla) perpendicolare alla superficie del campione, Zhu et al. osservato un forte ZBCP (picco di conduttanza zero-bias) in un nucleo di vortice. Come previsto per un MZM isolato in un vortice quantistico limitato, lo ZBCP non si è disperso o diviso attraverso il nucleo del vortice. Hanno eseguito misurazioni dipendenti dall'accoppiamento del tunnel sullo ZBCP osservato, aggiungendo la punta STM al centro di un vortice topologico, per registrare una serie di dI/dV spettri corrispondenti alla densità elettronica degli stati nella posizione della punta, per diverse distanze punta-campione. Hanno osservato che lo ZBCP rimane come un picco ben definito situato a energia zero.
Per esaminare la simmetria particella-foro degli MZM, hanno confrontato e messo a confronto il comportamento di conduttanza di MZM a energia zero e CBS a energia finita (Stati legati di Caroli-de Gennes-Matricon). Zhu et al. osservato due distinti tipi di vortici topologici e ordinari con, o senza MZM, che differiva per uno spostamento di livello semiintero degli stati legati al vortice. Hanno eseguito misurazioni dipendenti dall'accoppiamento del tunnel su un vortice topologico per mostrare un MZM e il primo livello CBS, a 0 meV e ±0,3 meV, hanno anche condotto misurazioni su un vortice ordinario.
Quando il team di ricerca ha ripetuto gli esperimenti in campo magnetico zero nella stessa posizione, hanno osservato un duro, gap superconduttore. Gli scienziati hanno osservato solo la caratteristica del plateau di conduttanza in ZBCP, che indicava un comportamento unico dei modi Majorana. Il comportamento di plateau osservato nel lavoro ha fornito anche prove per la riflessione Andreev risonante indotta da Majorana. Successivamente, durante il tunneling di elettroni da un elettrodo normale attraverso una barriera in un superconduttore, il team ha osservato che il processo di riflessione di Andreev converte l'elettrone incidente in un foro in uscita all'interno dello stesso elettrodo. Ciò ha portato a un sistema a doppia barriera nello spazio di Hilbert particella-foro (uno spazio vettoriale astratto in meccanica quantistica).
Nel caso della riflessione di Andreev attraverso un singolo MZM, uguali ampiezze delle componenti particella/foro dovute all'equivalenza particella-antiparticella degli MZM assicuravano un identico accoppiamento del tunnel, con l'elettrone e la lacuna nello stesso elettrodo (Γ e = h ). Di conseguenza, la riflessione risonante Andreev mediata attraverso un singolo MZM ha portato a un 2e 2 Plateau di conduttanza zero bias quantizzato /h. In contrasto, CBS a bassa energia e altri stati banali di sub-gap non contengono simmetria di Majorana e la relazione tra l'elettrone e la lacuna è interrotta in una riflessione Andreev mediata dalla CBS, causando l'assenza di un plateau di conduttanza. Per di più, quando Zhu et al. rimosso il campo magnetico nel sistema sperimentale, il plateau di conduttanza a polarizzazione zero osservato nel nucleo del vortice è scomparso, quindi le osservazioni non potevano essere accreditate al trasporto balistico quantistico.
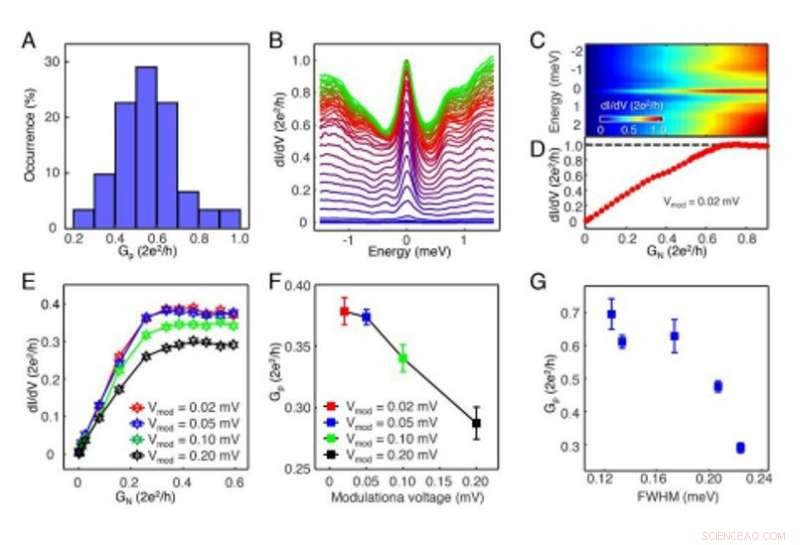
La variazione di conduttanza dell'altopiano di Majorana. (A) Un istogramma della Gp da 31 serie di dati misurati con lo stesso strumento. Si può trovare l'ordinamento della conduttanza del plateau (Gp) in ordine di ingrandimento crescente (Vs=-5mV, Vmod =0,02 mV). (B) La trama sovrapposta di 38 spettri dI/dV selezionati da un vortice topologico che ha raggiunto un plateau di conduttanza quantizzata (Vs=-5mV, Vmod =0,02 mV). (C) Un grafico in scala di colori di (B) con l'intervallo di energia di [-2,5, 2.5] meV che mostra gli spettri in funzione di GN. (D) Un taglio di linea orizzontale allo zero bias da (C). La curva di conduttanza mostra il raggiungimento del plateau di conduttanza G0. (E) Una serie di misurazioni dipendenti dall'accoppiamento del tunnel sullo stesso MZM, con quattro tensioni di modulazione di 0,02 mV, 0,05 mV, 0,10 mV e 0,20 mV. (F) Il grafico di Gp in funzione della tensione di modulazione dei dati mostrati in (E). (G) Relazione tra la metà massima dell'onda intera di ZBCP e Gp, ottenuto da cinque diversi MZM misurati nelle stesse condizioni sperimentali, suggerendo che l'effetto di equilibrio della quasiparticella influenza il valore di plateau. I FWHM sono stati estratti dallo spettro misurato a grande distanza punta-campione con gli stessi parametri sperimentali (Vs=-5 mV, esso =500 pA, Vmod =0,02 mV). Credito: Scienza , doi:10.1126/science.aax0274
Gli scienziati hanno osservato ripetutamente il comportamento di plateau degli ZBCP in molti vortici topologici attraverso 60 misurazioni. Per comprendere gli effetti dell'allargamento strumentale sugli altipiani di conduttanza di Majorana, gli scienziati hanno variato la tensione di modulazione (V modalità ). Questo ha permesso loro di studiare il V modalità -evoluzione dei plateau di conduttanza di Majorana su un dato vortice topologico. Zhu et al. quindi testato la reversibilità del processo variando l'accoppiamento di tunneling in STM. Hanno scoperto che sia la topografia che il plateau di conduttanza potrebbero essere riprodotti dopo due sequenze ripetute per indicare l'assenza di danni irreversibili della punta e del campione durante le misurazioni. Il team di ricerca richiede ulteriori sforzi teorici per raccogliere una comprensione completa degli esperimenti, in quanto non escludono altri meccanismi relativi ai plateau di conduttanza a polarizzazione zero.
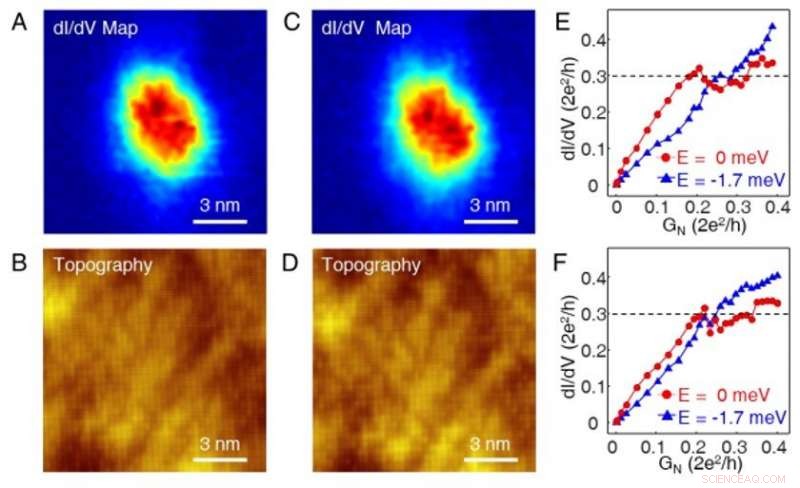
Reversibilità delle misure dipendenti dall'accoppiamento in galleria. (A)-(B) Una mappa dI/dV a polarizzazione zero e la corrispondente topografia STM misurata prima delle misurazioni dipendenti dall'accoppiamento del tunnel. La mappa e la topografia sono misurate nella stessa area. Il campo magnetico è 2.0 T. (C)-(D) Una mappa dI/dV a polarizzazione zero e la corrispondente topografia STM misurata dopo misurazioni dipendenti dall'accoppiamento del tunnel. Il campo magnetico è 2.0 T. I parametri di misura sono gli stessi di quelli in (A-B):bias del campione, Vs=–5 mV; corrente di tunneling, It=500 pA. (E)-(F) Due sequenze ripetute di misurazioni dipendenti dall'accoppiamento del tunnel nella stessa posizione spaziale, mostrando una conduttanza di plateau media di 0,30 G0, rispettivamente. I dati mostrati in (F) vengono registrati durante un secondo processo di avvicinamento alla punta dopo aver terminato il primo. Credito: Scienza , doi:10.1126/science.aax0274
In questo modo, l'osservazione di un plateau di conduttanza a polarizzazione zero in un vortice sperimentale bidimensionale si è avvicinata al valore di conduttanza quantizzata di 2e 2 /h. In questo lavoro, Shiyu Zhu e colleghi hanno fornito prove spettroscopiche risolte spazialmente per la trasmissione di elettroni risonanti indotta da Majorana in un superconduttore di massa. I risultati fanno un ulteriore passo avanti verso le applicazioni degli operatori di intreccio per descrivere gli entanglement topologici o le porte quantistiche universali per il calcolo quantistico topologico.
© 2019 Scienza X Rete