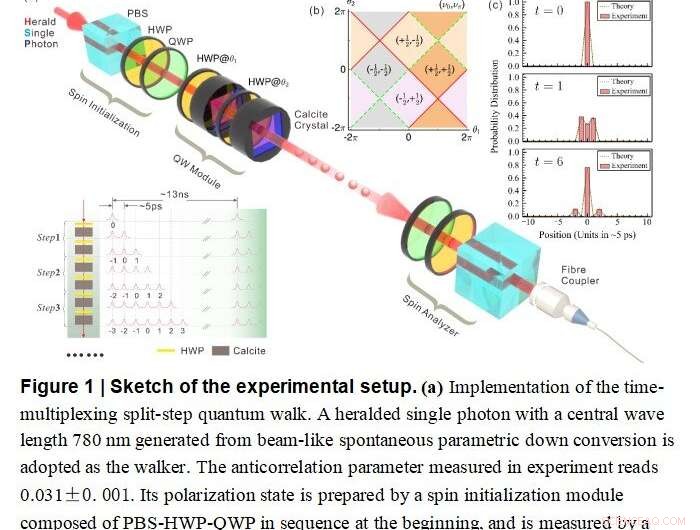
Schizzo del setup sperimentale Credito:di Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei Wei Pan, Zhe Chen, Munsif Jan, Kai Sole, Jin Shi Xu, Yong-Jian Han, Chuan Feng Li, Guang-Can Guo
I processi dinamici di non equilibrio sono centrali in molti contesti tecnologici quantistici. Però, è rimasta una sfida chiave identificare i concetti per la loro caratterizzazione e classificazione, poiché gli stati quantistici risultanti sfidano volutamente una descrizione in termini di fisica statistica dell'equilibrio al fine di realizzare stati non accessibili con mezzi convenzionali. Gli scienziati hanno ora ottenuto una caratterizzazione in termini di un parametro di ordine topologico dinamico per le passeggiate quantistiche, che rappresentano una classe paradigmatica di processi di non equilibrio.
La coerenza nella dinamica quantistica è al centro di affascinanti fenomeni al di là del regno della fisica classica, come effetti di interferenza quantistica, produzione di entanglement e fasi geometriche.
I processi quantistici di natura dinamica intrinseca sfidano una descrizione in termini di un insieme di fisica statistica dell'equilibrio. Fino ad ora, identificare i principi generali alla base della dinamica quantistica unitaria sottostante che preservano la coerenza quantistica rimane una sfida chiave.
Le passeggiate quantistiche forniscono una piattaforma potente e flessibile per realizzare sperimentalmente e sondare l'evoluzione temporale quantistica coerente lontano dall'equilibrio termico. A differenza delle classiche passeggiate casuali, le passeggiate quantistiche sono caratterizzate da sovrapposizioni quantistiche di ampiezze piuttosto che da distribuzioni di probabilità classiche. Questo autentico carattere quantistico è già stato sfruttato in vari campi della fisica, che vanno dalla progettazione di algoritmi efficienti nell'elaborazione dell'informazione quantistica, osservazione di dinamiche correlate e localizzazione di Anderson, alla realizzazione di fenomeni fisici esotici nelle fasi topologiche di contesto.
Mentre l'ordine topologico può essere recuperato nello spazio reale, l'accesso all'intera e complessa informazione di ampiezza che caratterizza la sovrapposizione coerente rimane una delle sfide chiave negli esperimenti di camminata quantistica.
In un nuovo articolo pubblicato su Scienza e applicazione della luce , scienziati del CAS Key Laboratory of Quantum Information e collaboratori internazionali hanno riferito sull'osservazione diretta di un parametro di ordine topologico dinamico (DTOP) che fornisce una caratterizzazione dinamica delle passeggiate quantistiche.
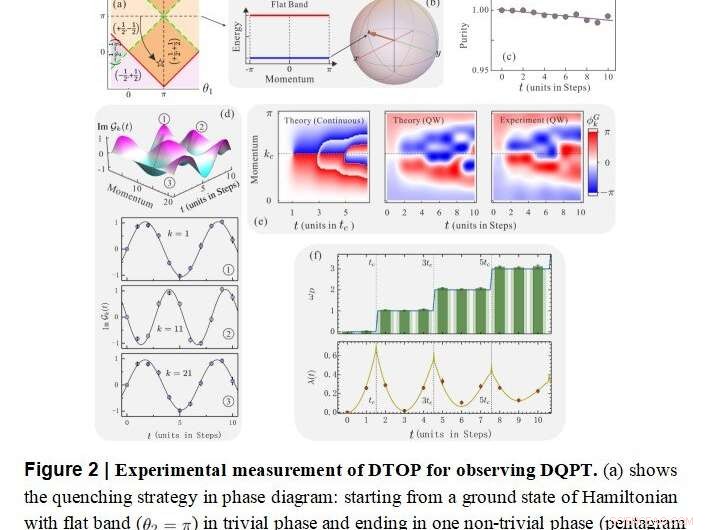
Misura sperimentale del DTOP per l'osservazione del DQPT Credito:di Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei Wei Pan, Zhe Chen, Munsif Jan, Kai Sole, Jin Shi Xu, Yong-Jian Han, Chuan Feng Li, Guang-Can Guo
A tal fine, hanno realizzato una passeggiata quantistica a passo diviso in un sistema fotonico utilizzando la struttura del multiplexing temporale. Utilizzando una tecnica precedentemente sviluppata, hanno ottenuto la tomografia a stato completo dello stato quantico evoluto nel tempo per un massimo di 10 fasi temporali complete. È importante sottolineare che questo ha fornito l'intera e complessa informazione sull'ampiezza dello stato della passeggiata quantistica.
"Questo è essenziale per il nostro obiettivo centrale di una classificazione dinamica della passeggiata quantistica utilizzando il DTOP, poiché il DTOP misura il numero di avvolgimento di fase _D (t) nello spazio del momento, vale a dire della cosiddetta fase geometrica Pancharatnam (PGP)".
Dai risultati sperimentali, hanno scoperto che le transizioni dinamiche tra classi topologicamente distinte di passeggiate quantistiche possono essere distinte in modo univoco dal comportamento osservato dipendente dal tempo di _D (t).
"Per un quench tra due sistemi con lo stesso carattere topologico, troviamo ω_D (t)=0 per tutti i passi temporali; Invece, per un quench tra due sistemi topologicamente diversi, Anche ω_D (t) inizia da ω_D (t=0)=0, ma cambia monotonamente il suo valore in certi momenti critici, " hanno aggiunto.
Generalizzando queste osservazioni, hanno inoltre stabilito una relazione unica tra il comportamento di ω_D (t) e il cambiamento di un parametro quench nelle proprietà topologiche di un'efficace Hamiltoniana di Floquet che descrive stroboscopicamente il cammino quantistico.
Gli scienziati concludono:"In questo modo, forniamo una prospettiva di non equilibrio sulle passeggiate quantistiche, che può essere inteso come un punto di partenza per avvicinarsi ai processi dipendenti dal tempo da un'angolazione intrinsecamente dinamica che va oltre la nozione di fisica statistica dell'equilibrio. Con questo e la mappatura sui quench in un sistema quantistico a molti corpi equivalente, il nostro esperimento offre una piattaforma versatile per studiare le dinamiche di non equilibrio coerenti di molti modelli paradigmatici come il modello Su-Schrieffer-Heeger, la catena Kitaev dell'onda p, o il modello di Ising a campo trasversale in futuro."