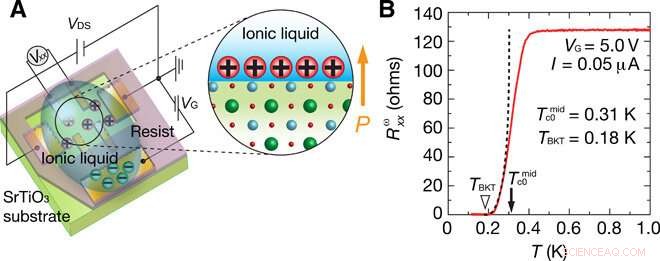
Immagine del dispositivo e superconduttività indotta da gate in SrTiO3. (A) Immagine schematica di SrTiO3-EDLT. (B) Resistenza longitudinale della prima armonica Rωxx in funzione della temperatura T sotto zero campo magnetico. La corrente applicata era 0,05 μA, che può essere considerato un limite di bassa corrente. La temperatura di transizione definita dal punto medio della transizione resistiva è stimata come Tc0 =0,31 K (freccia nera). La linea tratteggiata nera mostra la curva di adattamento secondo la formula Halperin-Nelson, dove RN =128 ohm è la resistenza allo stato normale (T =1,0 K), b =1.17 è una costante adimensionale, e TBKT =0,18 K è la temperatura di transizione BKT (triangolo bianco). La tensione di gate applicata VG è 5,0 V a T =260 K. Credito:Science Advances, doi:10.1126/sciadv.aay9120
Nella scienza dei materiali, i sistemi elettronici bidimensionali (2DES) realizzati sulla superficie o sull'interfaccia dell'ossido sono un candidato promettente per ottenere nuove proprietà fisiche e funzionalità in un campo quantistico in rapida espansione. Mentre 2-DES fornisce un'importante piattaforma per eventi quantistici esotici tra cui l'effetto Hall quantistico e la superconduttività, l'effetto della rottura della simmetria; transizione da uno stato disordinato a uno stato più definito, su tali fasi quantistiche rimangono sfuggenti. Il trasporto elettrico non reciproco o la resistenza dipendente dalla direzione della corrente è una sonda per la simmetria di inversione rotta (presenza di un dipolo), come osservato su diversi cristalli e interfacce non centrosimmetrici. In un nuovo rapporto, Yuki M. Itahashi e un team di scienziati in fisica applicata, nanosistemi e scienza dei materiali in Giappone e negli Stati Uniti hanno riportato il trasporto non reciproco sulla superficie di un superconduttore 2-D realizzato con il materiale superconduttore titanato di stronzio (SrTiO 3 ). Il team ha osservato un gigantesco miglioramento della regione non reciproca nella regione di fluttuazione superconduttiva, a sei ordini di grandezza più grande rispetto al suo stato normale. I risultati sono ora pubblicati su Progressi scientifici e dimostrare caratteristiche senza precedenti del superconduttore polare 2-D.
I conduttori polari o superconduttori sono potenziali piattaforme materiali per il trasporto quantistico e le funzionalità spintroniche, con intrinseco trasporto non reciproco che riflette la proprietà sfuggente della rottura della simmetria di inversione temporale (cioè rottura della conservazione dell'entropia). Esperimenti recenti si sono estesi allo stato superconduttore per osservare una grande risposta non reciproca ei fisici sono desiderosi di esaminare la non reciprocità intorno alla transizione superconduttiva in un semplice sistema di elettroni. Per questo, Itahash et al. elettrodi ingegnerizzati di cromo/oro (Cr/Au) sulla superficie atomicamente piatta di SrTiO 3 e posto del liquido ionico sulla parte superiore per formare un transistor elettrico a doppio strato (EDLT) per realizzare un superconduttore Rashba; sulla base dell'effetto Rashba, con una tecnica di ion-gating su SrTiO 3 superficie del materiale. Gli scienziati hanno quindi misurato il trasporto elettronico della prima e della seconda armonica utilizzando una tecnica standard di lock-in per misurare il trasporto di carica non reciproco e quantificare la rottura della simmetria di inversione temporale nel sistema. Il trasporto non reciproco è anche uno strumento efficace per identificare coppie Cooper, dove una coppia di elettroni supera la loro solita repulsione per condividere uno stato quantico per la paraconduttività non reciproca nei superconduttori, quale Itahashi et al. anche destinato a quantificare nel superconduttore Rashba.
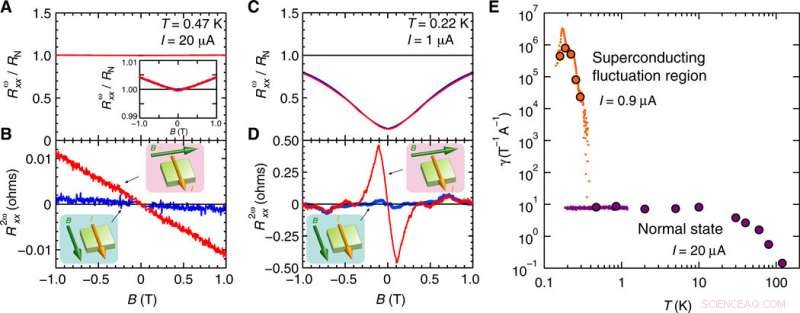
Magnetotrasporto di SrTiO3 2D indotto da gate sia per lo stato normale che superconduttore e potenziamento del trasporto non reciproco nella regione di fluttuazione superconduttiva. (A) Magnetoresistenza di prima e (B) seconda armonica (Rωxx e R2ωxx, rispettivamente) sopra Tc0 (stato normale, T =0,47 K e I =20 μA) in funzione del campo magnetico nel piano B perpendicolare (rosso) o parallelo (blu) a I. I riquadri in (A) e (B) mostrano la vista ingrandita di Rωxx(B) e schemi della configurazione di misura (direzioni di B e I), rispettivamente. (C) Rωxx e (D) R2ωxx al di sotto di Tc0 (regione di fluttuazione superconduttiva, T =0,22 K e I =1 μA) in funzione del piano B perpendicolare (rosso) o parallelo (blu) a I. In (A) a (D), Rωxx è normalizzato dalla resistenza allo stato normale RN =128 ohm, e Rωxx/R2ωxx è simmetrico/antisimmetrico in funzione di B. (E) Dipendenza dalla temperatura di γ=2R2ωxxRωxxBI nello stato normale (I =20 μA) e nella regione di fluttuazione superconduttiva (I =0,9 μA). I cerchi viola (stato normale) e arancioni (regione di fluttuazione superconduttiva) sono stati estratti dalla misurazione della scansione del campo magnetico di R2ωxx a bassa B inferiore a 0,1 T, mentre i punti viola (stato normale) e arancioni (regione di fluttuazione superconduttiva) sono stati tracciati dalla scansione della temperatura di R2ωxx sotto B =3 e 0,05 T, rispettivamente. Credito:progressi scientifici, doi:10.1126/sciadv.aay9120
Gli scienziati inizialmente hanno dettagliato la prima resistenza armonica (FHR) corrispondente alla resistenza lineare vicino alla transizione superconduttiva per una tensione di gate di 5,0 V. I risultati hanno mostrato una dipendenza dalla temperatura al limite di corrente basso (I =0,05 μA). Quindi si sono concentrati sulla resistenza della seconda armonica (SHR) e sul trasporto di carica non reciproco accreditato osservato sulla superficie di SrTiO 3 alla simmetria polare all'interno della regione di fluttuazione superconduttiva e nello stato normale. Il team ha osservato il trasporto magnetico in SrTiO . 2-D indotto da gate 3 all'interno di un campo magnetico (B) perpendicolare alla corrente (I) per stati normali e superconduttori, con trasporto non reciproco potenziato nella regione di fluttuazione superconduttiva. Per confrontare l'entità della non reciprocità tra lo stato normale e la regione di fluttuazione della superconduttività, hanno calcolato il coefficiente di magnetoresistenza non reciproca (γ), che dipendeva dalla temperatura all'interno delle regioni.
Il team ha successivamente misurato la dipendenza dei segnali della seconda armonica dalla corrente (I), nello stato normale e nella regione di fluttuazione superconduttiva. Nello stato normale, l'SHR ha mostrato una dipendenza quasi lineare dalla corrente. Nella regione di fluttuazione della superconduttività a un campo magnetico di 0,1 Tesla, l'SHR è aumentato linearmente, raggiunto un massimo a circa 1 µA e soppresso, per indicare la soppressione della superconduttività da parte dell'alta corrente.
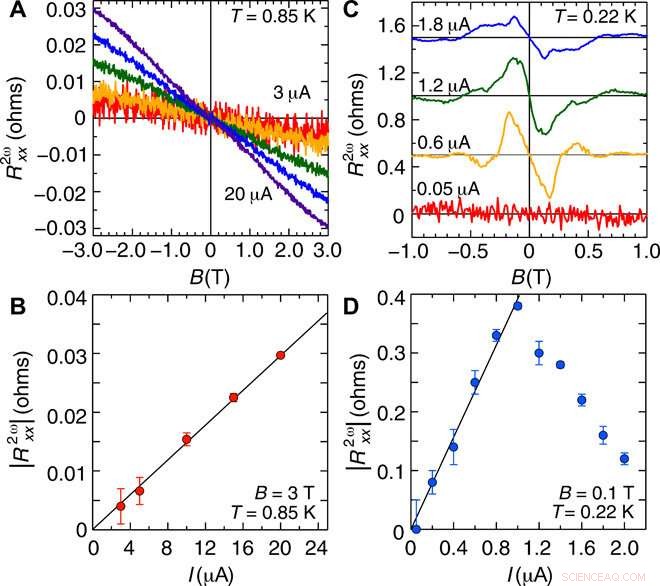
Dipendenza dalla corrente della magnetoresistenza di seconda armonica nella regione di fluttuazione normale e superconduttiva. (A) Magnetoresistenza della seconda armonica R2ωxx a T =0,85 K sotto I =3 μA (rosso), 5 μA (arancione), 10 μA (verde), 15 μA (blu), e 20 μA (viola). R2ωxx è antisimmetrizzato in funzione di B. (B) ∣∣R2ωxx∣∣ a B =3 T in funzione di I, che viene estratto da (A). La linea continua nera mostra l'adattamento lineare in funzione di I. (C) Dipendenza dal campo magnetico di ∣∣R2ωxx∣∣ a T =0,22 K sotto I =0,05 μA (rosso), 0,6 μA (arancione), 1,2 μA (verde), e 1,8 μA (blu). Ogni curva è spostata verticalmente di 0,5 ohm e antisimmetrica in funzione di B. (D) Dipendenza dalla corrente di ∣∣R2ωxx∣∣ a B =0,1 T, dove R2ωxx è considerato una funzione lineare di B. Nella regione a bassa corrente (I ≤ 1 μA), ∣∣R2ωxx∣∣ aumenta linearmente (linea continua nera) con I. Credito:Science Advances, doi:10.1126/sciadv.aay9120
Per indagare ulteriormente sulla possibile origine del trasporto superconduttore non reciproco nel sistema, gli scienziati hanno misurato la dipendenza dalla temperatura di FHR e SHR durante la transizione. Per realizzare questo, hanno notato la dipendenza dal campo magnetico di FHR e SHR a varie temperature e hanno osservato in modo specifico che l'SHR è ampiamente migliorato durante il trasporto superconduttore. Sebbene Itahashi et al. applicato una corrente relativamente grande e un campo magnetico nel piano, hanno registrato lo stato di resistenza zero alla temperatura più bassa. I risultati implicavano l'esistenza della transizione Berenzinskii-Kosterlitz-Thouless (transizione BKT), prende il nome da un team di fisici della materia condensata vincitori del premio Nobel. Descrive le transizioni di fase nei sistemi 2-D nella fisica della materia condensata approssimate da un modello XY per comprendere fasi o stati insoliti della materia nei superconduttori.
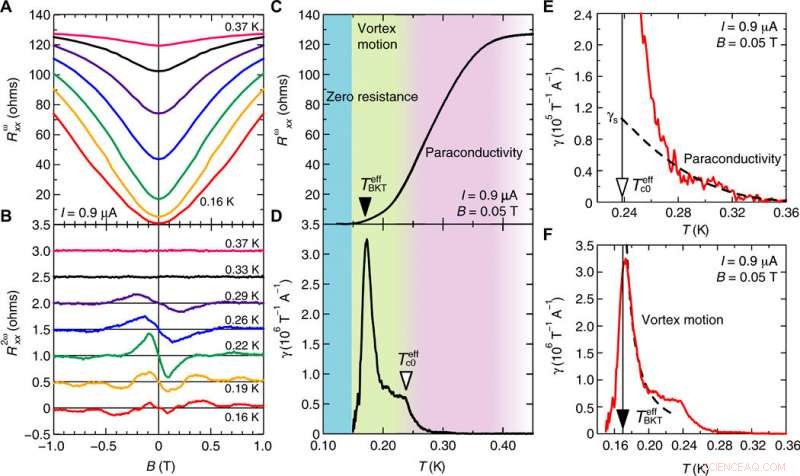
Dipendenza dalla temperatura della magnetoresistenza e del trasporto non reciproco. Dipendenza dal campo magnetico di (A) la prima (Rωxx) e (B) la seconda (R2ωxx) magnetoresistenza armonica a T =0,16 K (rosso), 0,19 K (arancione), 0,22 K (verde), 0,26 K (blu), 0,29 K (viola), 0,33 K (nero), e 0,37 K (rosa), rispettivamente. In (B), ogni curva viene spostata verticalmente di 0,5 ohm. Rωxx/R2ωxx è simmetrico/antisimmetrico in funzione di B. Variazione di temperatura di (C) Rωxx e (D) γ sotto B =0,05 T e I =0,9 μA. In questa regione, R2ωxx è lineare in funzione di B e I. Rωxx/γ è simmetrico/antisimmetrico in funzione di B. La struttura caratteristica (struttura kink intorno a T =0,24 K e struttura del picco intorno a T =0,17 K) appare in (D), secondo cui possiamo identificare due regioni del trasporto non reciproco di diversa origine, cioè., regione di paraconduttività e regione di vortice. Alla temperatura più bassa, si osserva lo stato di resistenza zero, dove Rωxx e diventa trascurabilmente piccolo. Ingrandimento di nella regione di paraconduttività (E) e nella regione di vortice (F). La linea tratteggiata nera in (E) mostra la curva di adattamento di γ(T)=γs(1−R(T)RN)2, e la linea tratteggiata nera in (F) indica la curva di adattamento di (T)=C(T−TeffBKT)−3/2. La resistenza allo stato normale RN =128 ohm è definita come Rωxx a T =1,0 K. Credito:Science Advances, doi:10.1126/sciadv.aay9120
In questo modo, Yuki M. Itahashi e colleghi hanno proposto il trasporto non reciproco in superconduttori 2-D non centrosimmetrici (senza simmetria di inversione) all'interno di un campo magnetico. Il trasporto non reciproco è originato dalla fluttuazione di ampiezza dallo stato normale a quello superconduttore. La dipendenza dalla temperatura del coefficiente di magnetoresistenza non reciproca (γ) osservato negli esperimenti concordava bene con l'immagine teorica microscopica del movimento libero per vortici e antivortici termicamente eccitati nei superconduttori polari 2-D. La risposta non reciproca è quindi un potente strumento per comprendere la natura dei superconduttori non centrosimmetrici.
Itahash et al. credono che il trasporto non reciproco possa apparire universalmente per materiali diversi in sistemi superconduttori interfacciali con simmetria polare. I risultati forniscono informazioni su funzioni precedentemente sconosciute della superconduttività e importanti informazioni sullo stato elettronico e sui meccanismi di accoppiamento nei superconduttori non centrosimmetrici, come argomento importante per ulteriori indagini. Il lavoro ha evidenziato il trasporto non reciproco in sistemi superconduttori interfacciali come il superconduttore 2-D indotto da gate SrTiO 3 . Il team ha sondato il marcato salto del trasporto non reciproco dallo stato normale a quello superconduttore come prova diretta di un gigantesco miglioramento del trasporto non reciproco nel sistema. I risultati offrono importanti informazioni sui superconduttori polari e aprono un nuovo modo per cercare proprietà e funzionalità emergenti finora sconosciute alle interfacce e ai superconduttori di ossido 2-D.
© 2020 Scienza X Rete