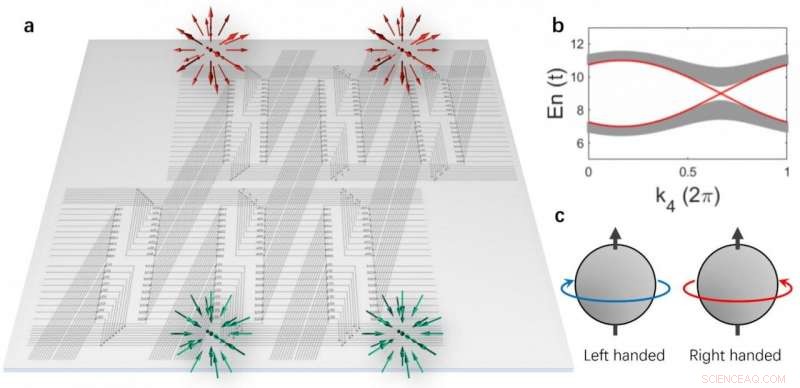
(a) Il reticolo circuitale 4D realizzato su un piano 2D. Una coppia di punti Weyl con la stessa chiralità sono localizzati sul confine tridimensionale. (b) Le strutture a banda di massa e gli stati di Weyl al confine (linee rosse). (c) Schema della chiralità degli stati di Weyl. Credito:Science China Press
Negli ultimi anni, la topologia è emersa come uno strumento importante per classificare e caratterizzare le proprietà dei materiali. È stato scoperto che molti materiali presentano una serie di proprietà topologiche insolite, che non sono interessati da deformazioni, per esempio., allungamento, compressione, o torsione. Queste proprietà topologiche includono correnti di Hall quantizzate, grande magnetoresistenza, ed eccitazioni superficiali che sono immuni al disturbo. Si spera che queste proprietà possano essere utilizzate per tecnologie future, come, elettronica a basso consumo, rilevatori ultraveloci, convertitori di energia ad alta efficienza, o per il calcolo quantistico.
Più recentemente, la topologia è stata applicata anche ai materiali sintetici, per esempio., cristalli fotonici o reti di circuiti elettrici. Questi materiali sintetici hanno diversi vantaggi rispetto alle loro controparti naturali. Per esempio, la topologia delle loro eccitazioni (cioè, loro bande di eccitazione) possono essere controllati e manipolati con precisione. Inoltre, grazie alla loro connettività reticolare a lungo raggio, i materiali sintetici possono realizzare eccitazioni topologiche di dimensioni maggiori di tre. Quindi, materiali sintetici, ed in particolare reti di circuiti elettrici, offrono la possibilità di realizzare una serie di proprietà topologiche interessanti che non sono accessibili nei materiali reali.
Rui Yu dell'Università di Wuhan, Yuxin Zhao dell'Università di Nanchino, e Andreas Schnyder del Max-Planck-Institute di Stoccarda hanno ora dimostrato questo potenziale costruendo esplicitamente una rete di circuiti elettrici che simula un isolante topologico quadridimensionale (4-D) con una classica simmetria di inversione temporale [Fig. 1(a)]. Gli isolanti topologici sono materiali isolanti nel volume sfuso, ma altamente conduttivo in superficie, a causa di eccitazioni superficiali gapless. Allo stesso modo, l'isolatore topologico 4-D simulato ha un gap di eccitazione nel volume di massa, all'interno della quale esiste una coppia di eccitazioni superficiali [Fig. 1(b)].
Queste eccitazioni superficiali 3-D hanno una dispersione lineare, e più interessante, sono di tipo Weyl con la stessa manualità, cioè., hanno gradi di libertà interni che ruotano seguendo la stessa regola sinistrorsa o destrorsa rispetto alla loro direzione di propagazione [Fig. 1(c)]. Sono di origine topologica e sono diverse da qualsiasi eccitazione superficiale che si trova nei materiali convenzionali. La topologia impone che queste eccitazioni di Weyl 3D debbano venire in coppia e che siano resistenti al disordine e alle deformazioni. Gli autori hanno eseguito simulazioni numeriche dettagliate della rete del circuito topologico e hanno dimostrato che le eccitazioni di Weyl 3D possono essere facilmente osservate nelle misurazioni dipendenti dalla frequenza.
Il lavoro degli autori dimostra che le eccitazioni topologiche possono essere facilmente realizzate su circuiti stampati disponibili in commercio o wafer di circuiti integrati composti da induttori e condensatori. Apre la strada alla realizzazione di tipi arbitrari di eccitazioni superficiali topologiche, Per esempio, le cosiddette eccitazioni di Dirac o Majorana di dimensione due, tre, o anche superiore. L'implementazione del circuito elettrico delle eccitazioni topologiche ha il vantaggio di essere semplice, facilmente riconfigurabile, e consentendo un alto grado di controllo. Ciò consentirà di studiare in futuro le transizioni di fase topologiche, effetti non lineari, fenomeni di fuori equilibrio, e sistemi quantistici aperti (ad es. sistemi non hermitiani).