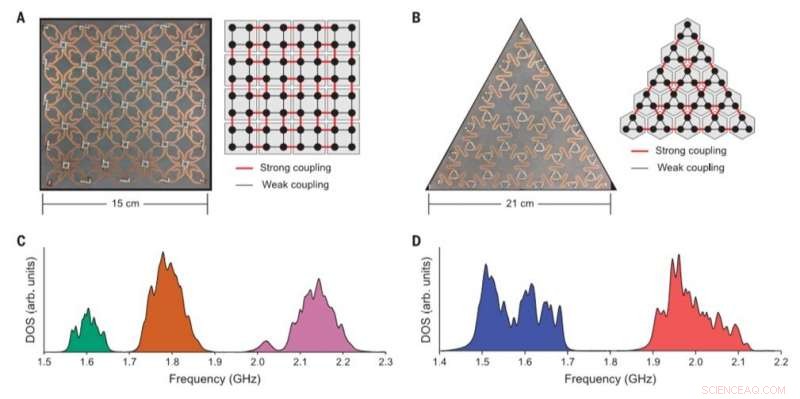
Un'anomalia dell'angolo frazionario rivela una topologia di ordine superiore

Metamateriali fabbricati e spettri misurati. (A) Fotografia della matrice di risonatori sperimentali con simmetria C4. Lo schema a destra illustra l'accoppiamento tra i risonatori. (B) Fotografia della matrice di risonatori sperimentali con simmetria C3. Lo schema a destra illustra l'accoppiamento tra i risonatori. (C) Spettro DOS misurato per l'array di risonatori in (A). arb. unità, unità arbitrarie. (D) Spettro DOS misurato per l'array di risonatori in (B). Credito:Scienza, doi:science.sciencemag.org/content/368/6495/1114

Gli isolanti topologici (TI) hanno un interno isolante e supportano stati superficiali conduttivi con proprietà di interfaccia aggiuntive. Gli stati metallici esotici sulle loro superfici possono fornire nuovi percorsi per generare nuove fasi e particelle con potenziali applicazioni nell'informatica quantistica e nella spintronica. I ricercatori hanno sviluppato un quadro teorico per aiutare a identificare e caratterizzare tali stati esotici utilizzando nuovi marcatori topologici come la densità di carica frazionaria per rilevare gli stati topologici della materia. L'accordo risultante tra lavoro sperimentale e teoria ha incoraggiato applicazioni su piattaforme topologiche. In questo lavoro, Christopher W. Peterson e un team di scienziati in ingegneria elettrica e informatica, fisica, e la scienza meccanica presso l'Università dell'Illinois e la Pennsylvania State University negli Stati Uniti discutono questo nuovo indicatore topologico introdotto per identificare la topologia di ordine superiore e dimostrare la corrispondenza di confine di massa di ordine superiore associata. L'opera è ora pubblicata su Scienza .

La topologia è una branca della matematica che studia le proprietà degli oggetti che sono invarianti (invariati) quando soggetti a deformazioni lisce. Gli isolanti topologici o i materiali con una struttura a bande divaricate (dove non possono esistere stati elettronici) possono essere caratterizzati da invarianti topologici, ovvero una proprietà preservata che non può cambiare finché il materiale rimane isolante, che può preservare il bandgap di massa e le simmetrie protettive nei materiali. Inoltre, la struttura a bande elettroniche di un solido contiene una gamma di livelli di energia con gli elettroni. Gli intervalli senza elettroni sono noti come bandgap; quest'ultimo definisce tipicamente intervalli di energia residua che non sono coperti da alcuna banda. Il campo matematico della topologia è quindi un quadro per studiare le strutture elettroniche a bassa energia dei solidi cristallini. Tipicamente una massa, il cristallo topologico tridimensionale isolante contiene uno stato superficiale bidimensionale conduttivo che facilita la corrispondenza topologica di massa-confine.

In questo studio, Peterson et al. focalizzato su TI bidimensionali. I materiali con invarianti protetti da simmetrie spaziali sono noti come isolanti topologici cristallini (TCI) e il team si è concentrato su una classe di TCI recentemente scoperta classificata come isolanti topologici di ordine superiore (HOTI). Finora, gli scienziati hanno identificato solo alcuni HOTI naturali conducendo molti studi sperimentali in metamateriali ingegnerizzati, comprese le reti di risonatori accoppiati, array di guide d'onda e cristalli fotonici o sonici. Avevano anche identificato l'indicatore più vicino di ordine superiore in tali sistemi utilizzando misurazioni spettroscopiche.

Però, esiste un problema fondamentale con tali tecniche spettrali poiché gli HOTI possono essere erroneamente identificati, anche quando i loro spettri non mostrano modalità in-gap. Di conseguenza, gli scienziati miravano a stabilire un indicatore misurabile sperimentalmente della topologia di ordine superiore protetta da simmetrie spaziali. In questo studio, sulla base di lavori precedenti, Peterson et al. hanno dimostrato come una caratteristica nei metamateriali possa essere quantizzata in modo frazionario per diagnosticare sia la topologia di primo ordine che quella di ordine superiore nei TCI con gap (isolanti cristallini topologici). Quando si studiano le due dimensioni, gli scienziati hanno chiamato la quantità che indica la topologia di secondo ordine come anomalia dell'angolo frazionario (FCA). Gli isolanti topologici di secondo ordine o gli isolanti cristallini contengono bulk gap e confini cristallini gapped con stati gapless topologicamente protetti all'intersezione dei due confini. Per osservare la FCA in via sperimentale, Peterson et al. costruito due metamateriali TI rotazionalmente simmetrici in array di risonatori accoppiati a microonde.

Hanno selezionato due isolanti con simmetrie diverse (quadrato e triangolo), poiché la quantizzazione della densità del modo frazionario e della FCA dipendeva dalla simmetria di rotazione del gruppo. Il team ha dimostrato il primo isolante su un reticolo quadrato con C ₄ simmetria e un secondo isolante su un reticolo kagome con C ₃ simmetria (forma triangolare). Hanno identificato la densità spettrale degli stati (DOS) di entrambi i metamateriali, utilizzando misure di riflessione. Gli spettri misurati del C ₄ -isolante simmetrico ha mostrato tre bande distinte, mentre il C ₃ -isolante simmetrico ha mostrato due bande. Poiché nessuno dei due isolanti aveva modalità in-gap, era difficile determinare se uno dei due metamateriali fosse topologicamente non banale basandosi solo sugli spettri.

Peterson et al. quindi calcolato la densità modale delle bande misurate includendo il DOS locale (densità di stati) in ogni cella unitaria. La densità modale del C ₄ -isolante simmetrico aveva diverse caratteristiche importanti, compresa la presenza di bande alla rinfusa, disordine di rottura della simmetria da imperfezioni di fabbricazione e una densità di modo frazionario diverso da zero nelle celle unitarie di bordo e d'angolo. Hanno estratto l'FCA (anomalia dell'angolo frazionario) per ciascuna banda bulk utilizzando i dati di densità della modalità. Poiché nell'esperimento con C . esisteva una piccola quantità di disordine inevitabile ₄ simmetria, hanno calcolato la media su tutti gli spigoli per trovare la densità di modo frazionario della cella unitaria di bordo (σ) e la media di tutti gli angoli per trovare la densità di modo frazionario della cella di unità d'angolo (ρ). Hanno calcolato in modo simile la densità modale per C ₃ -sistema simmetrico. L'FCA diverso da zero calcolato in entrambi i metamateriali indicava che erano entrambi HOTI (isolatori topologici di ordine superiore) con la capacità di ospitare modalità topologiche di secondo ordine ai loro angoli.

Peterson et al. notò i risonatori d'angolo attorno ai quali ci si aspettava che esistessero i modi topologici del secondo ordine, essere eccitato nella fascia tre del Do ₄ -sistema simmetrico. nel C ₃ -sistema simmetrico, i risonatori d'angolo erano eccitati solo nella seconda banda, indicando che l'energia delle modalità d'angolo è troppo alta. Gli scienziati potrebbero localizzare spettralmente i modi abbassando leggermente la frequenza di risonanza dei risonatori d'angolo. Il team ha applicato un piccolo potenziale negativo agli angoli per portare queste modalità nel bandgap. I risultati sperimentali hanno catturato efficacemente le caratteristiche topologiche fondamentali protette da simmetrie spaziali; perciò, gli scienziati si aspettano che i risultati aiutino a identificare sperimentalmente materiali con topologia di ordine superiore. I nuovi risultati aiuteranno semplicemente la conferma sperimentale di nuovi isolanti topologici.