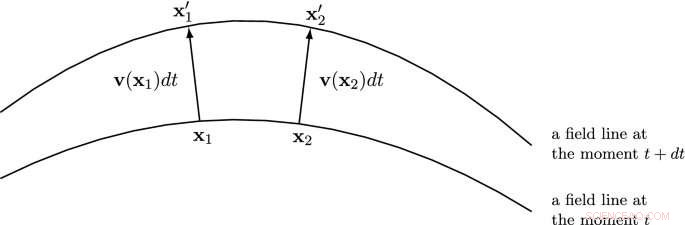
L'immagine mostra la condizione alla quale il campo vettoriale v deve obbedire per definire l'evoluzione temporale autoconsistente delle linee di campo. Per ogni due punti su una linea di campo al momento t le estremità dei vettori vdt nei punti corrispondenti giacciono su una linea di campo che è definita al momento t+dt DOI 10.1140/epjc/s10052-020-08745-7
Le equazioni di Maxwell governano l'evoluzione dei campi elettromagnetici con la luce che è una soluzione particolare di queste equazioni in spazi privi di carica elettrica. Un nuovo studio pubblicato su EPJ DO di Alexi Morozov e Nikita Tselousov, dall'Istituto di fisica e tecnologia di Mosca e dall'Istituto di problemi di trasmissione, Russia, rispettivamente, dettaglia soluzioni peculiari alle equazioni di Maxwell, i cosiddetti nodi di Maxwell. La ricerca potrebbe avere applicazioni nei campi della fisica matematica e della teoria delle stringhe.
"Di solito pensiamo alla luce come alle onde piane. È stata una svolta quando sono state scoperte soluzioni di luce "annodate", " spiega Tselousov. "La natura del nodo di queste soluzioni consiste nella struttura delle linee del campo elettrico e magnetico. Si può osservare che alcune delle linee di campo sono anelli chiusi e annodati in modo non banale".
Le linee del campo elettrico e magnetico cambiano nel tempo obbedendo alle equazioni di Maxwell. Quando i campi cambiano, le loro linee di campo si muovono in qualche modo nello spazio. Sebbene i ricercatori non possano tracciare una linea di campo arbitraria, le linee di campo chiuso sono speciali e possono essere osservate mentre si evolvono nel tempo.
"Nel nostro giornale, facciamo una congettura, che le linee di campo annodate si muovono in un modo molto speciale in cui la struttura annodata rimane, " Tselousov continua. "In altre parole, si può dire che questa volta l'evoluzione non comporti mai auto-attraversamenti o incroci di due linee di campo."
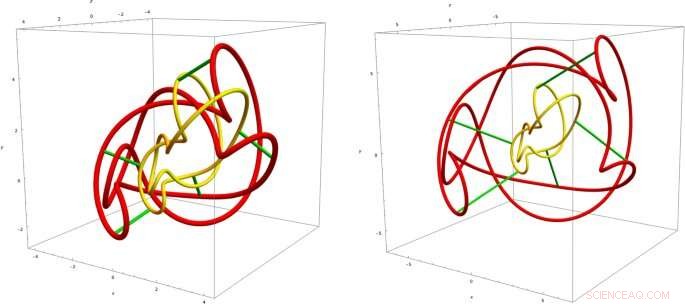
Il piccolo nodo giallo diventa quello grande rosso sotto l'evoluzione del tempo. Ci sono immagini di due momenti successivi del tempo. Le curve verdi sono le traiettorie. La struttura topologica del nodo non cambia sotto l'evoluzione temporale DOI 10.1140/epjc/s10052-020-08745-7
Tselousov ritiene che se questa congettura, ottenuta con l'uso di complesse simulazioni al computer, fosse corretta, la conservazione dei nodi implica che la loro evoluzione sia integrabile, capace di subire l'integrazione della funzione matematica. Ciò significa che la sua evoluzione può essere correlata ad altri modelli e sistemi, in particolare con equazioni non lineari, che sono noti per condividere questa proprietà.
"È molto raro e sempre un piacere osservare le proprietà integrabili dei sistemi perché significa una comprensione più profonda e possibili ulteriori progressi. Abbiamo intenzione di muoverci in questa direzione e trovare più connessioni con l'integrabilità, " Tselousov conclude. "Nella mia mente, uno dei fatti sbalorditivi è quella luce, così familiare a tutti, nascondere segreti che abbiamo ignorato per secoli."
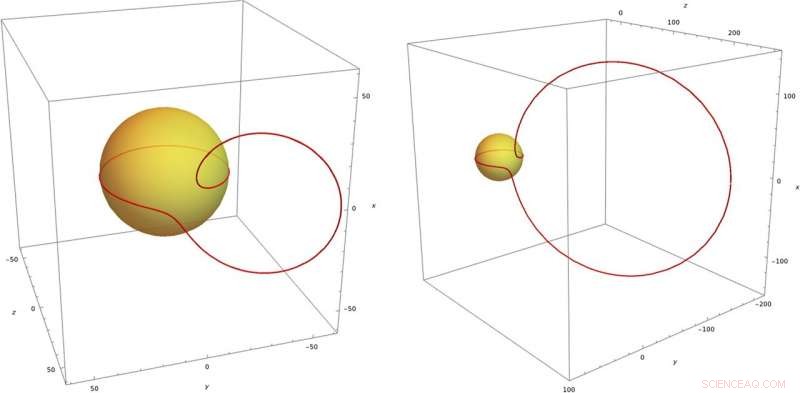
La sfera gialla è il cono di luce x2+y2+z2=t2x2+y2+z2=t2. Le linee rosse sono linee di campo elettrico al momento t=30t=30. Una parte della linea di campo giace sull'equatore della sfera. L'altra parte tende a formare un cerchio DOI 10.1140/epjc/s10052-020-08745-7