
In questo esempio, un angolo del triangolo è frustrato. Credito:Johan Jarnestad/The Royal Swedish Academy of Sciences, CC BY-NC
Il Premio Nobel per la Fisica 2021 è stato assegnato congiuntamente all'italiano Giorgio Parisi, Il giapponese Syukuro Manabe e il tedesco Klaus Hasselmann per i loro "contributi rivoluzionari alla nostra comprensione dei sistemi complessi".
Quando ho sentito la notizia, Non potevo crederci. Ho studiato per la mia tesi di master e il mio dottorato di ricerca. in fisica teorica sotto il professor Parisi all'Università La Sapienza di Roma.
Quando dico che ero incredulo, non fraintendermi. Di tutte le persone che ho incontrato nella mia esperienza di ricerca, forse nella mia vita, lui è senza dubbio il più ingegnoso. Quindi non sono rimasto sorpreso dalla decisione del comitato del Premio Nobel di nominarlo vincitore. Piuttosto, è stata la loro decisione di riconoscere i suoi "contributi alla nostra comprensione dei sistemi complessi" che ha suscitato il mio interesse.
Questo premio per il professor Parisi, diviso con i meteorologi pionieri, il professor Manabe e il professor Hasselmann, è un sorprendente riconoscimento di un'intera area di ricerca - forse un po' meno affascinante di quelle della relatività generale o della teoria delle stringhe - che tenta di comprendere e modellare ciò che in fisica chiamiamo "sistemi complessi".
Questi includono cose come gli ecosistemi climatici, sistemi finanziari, e fenomeni biologici, per dirne alcuni. L'assoluta varietà di sistemi complessi - rappresentati in mercati fluttuanti e storni affollati - rende molto difficile derivare per loro qualsiasi tipo di regole universali. Il lavoro di Parisi ha permesso di trarre conclusioni inedite su tali sistemi che, sulla superficie, sembrare casuale, imprevedibile e impossibile da modellare teoricamente.
A differenza di altri modelli fisici, i sistemi complessi non sono un insieme di particelle identiche, interagendo regolarmente in modo coerente e prevedibile. Anziché, i sistemi complessi sono sistemi di elementi, potenzialmente diversi tra loro, interagiscono in modi diversi e apparentemente imprevedibili mentre sono esposti a condizioni esterne variabili.
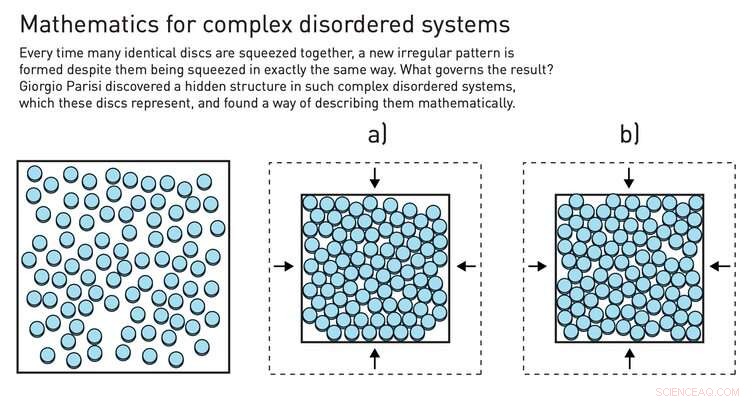
Il trucco della replica può essere condotto comprimendo le palline in una scatola. Credito:Johan Jarnestad/The Royal Swedish Academy of Sciences, CC BY-NC
Un trampolino di lancio per la modellazione di sistemi complessi è la teoria dei "sistemi disordinati". Questi sono essenzialmente sistemi in cui diverse coppie di elementi sperimentano differenti, forze potenzialmente conflittuali che possono portare gli elementi a diventare "frustrati".
Un modo per illustrarlo è immaginare un partito (un sistema sociale chiuso), dove Alice potrebbe voler chattare con Bob, e Bob potrebbe voler chattare con Charlie, ma Charlie potrebbe non voler chattare con Alice. C'è frustrazione qui, quindi cosa dovrebbero fare?
La ricerca del professor Parisi ha chiarito cosa succede quando la frustrazione si manifesta in sistemi disordinati e complessi. Ha identificato che i sistemi complessi sono in grado di ricordare le loro traiettorie nel tempo, e può rimanere bloccato in stati non ottimali per lungo tempo.
Nel nostro esempio di partito, immagina Alice, Bob, Charlie, e altri ospiti che cambiano in modo irregolare gruppi di conversazione e partner, sperando di trovare il miglior gruppo di persone con cui chattare, ma potenzialmente non trovandolo mai. Questo è lo stato sub-ottimale in cui i sistemi complessi possono rimanere bloccati.
Modelli dal disordine
Uno dei tanti strumenti teorici che il professor Parisi ha usato per stabilire la sua teoria è il cosiddetto "trucco della replica", un metodo matematico che prende un sistema disordinato, lo replica più volte, e confronta il comportamento delle diverse repliche del sistema. Puoi farlo, ad esempio, comprimendo le biglie in una scatola, che formerà una configurazione diversa ogni volta che si esegue la compressione. In molte ripetizioni, Parisi sapeva, potrebbero emergere schemi narrativi.
Questo metodo è oggi uno dei pochi pilastri teorici per lo sviluppo dell'intera teoria dei sistemi complessi come la conosciamo oggi. La teoria del professor Parisi ha dimostrato di fornire previsioni affidabili sulle proprietà statistiche di sistemi complessi che vanno dai liquidi superraffreddati (liquidi al di sotto della loro temperatura di solidificazione), liquidi congelati, solidi amorfi come il vetro, e persino stormi di storni.
La teoria dei sistemi disordinati ci permette di dare un senso alla bella comparsa di schemi di volo coerenti all'interno di stretti stormi di uccelli, che riescono a rimanere uniti e formare vasti gruppi nonostante le condizioni avverse.
La stessa struttura è stata utilizzata per dare un senso al clima terrestre. I meteorologi che condividono il premio Nobel con il professor Parisi avranno fatto affidamento sulle scoperte della fisica teorica per produrre i modelli che ora usiamo per dimostrare in modo affidabile il riscaldamento globale.
Ho avuto modo di discutere questi temi con il Professor Parisi a Roma, mentre si svolgevano i suoi esperimenti con gli stormi di uccelli e durante le sue simulazioni al computer sul comportamento del vetro. Conoscendo un po' della sua mente, Non sono affatto sorpreso che sia stato insignito del premio Nobel per la fisica.
Ma sono piacevolmente sorpreso che il campo dei sistemi complessi, che sta silenziosamente spingendo alla frontiera della ricerca teorica in fisica, è stata data questa esposizione. Questo premio Nobel ha conferito nuova legittimità e, possiamo sperare, nuove menti, in questa affascinante area della fisica contemporanea.
Questo articolo è stato ripubblicato da The Conversation con una licenza Creative Commons. Leggi l'articolo originale. 