In geometria, un esagono è un poligono con sei lati. Un esagono regolare ha sei lati uguali e angoli uguali. L'esagono regolare è comunemente riconosciuto dal nido d'ape e dall'interno della stella di David. Un esaedro è un poliedro a sei facce. Un esaedro regolare ha sei triangoli con bordi di uguale lunghezza. In altre parole, è un cubo.

Formula area esagonale

La formula per l'area di un esagono regolare con lati di lunghezza "a" è 3 --- sqrt (3) - - a ^ 2/2, dove "sqrt" indica la radice quadrata.

Derivation

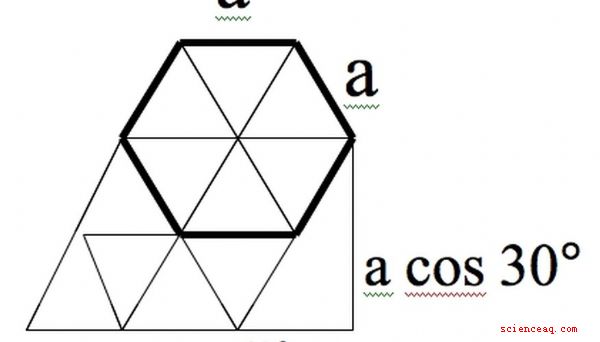
Un esagono regolare può essere visto come sei triangoli equilateri di lati a. I loro angoli sono 60 gradi, quindi gli angoli nell'esagono sono 120 gradi. I triangoli possono essere estesi sotto l'esagono per formare un parallelogramma dei lati 2a. Un triangolo più grande può essere creato per determinare l'altezza di questo parallelogramma, che è 2a --- cos 30 ° = a --- sqrt (3).

Il parallelogramma nella figura è quindi di altezza area - - base = (a --- sqrt (3)) --- 2a = 2 --- sqrt (3) --- a ^ 2.

Ma questo è per un parallelogramma composto da 8 triangoli equilateri. L'esagono era composto solo da 6. Quindi l'area dell'esagono è 0.75 di questa, o 3 --- sqrt (3) --- a ^ 2 /2.

Derivazione alternativa

sei triangoli equilateri in un esagono hanno i lati "a". Le loro altezze, h, sono, secondo il teorema di Pitagora, sqrt [a ^ 2 - (a /2) ^ 2] = a --- sqrt (3) /2.

L'area di un triangolo è quindi (½) --- base --- altezza = (a) --- [a --- sqrt (3) /4]. Sei triangoli nell'esagono danno un'area di 3 --- sqrt (3) --- a ^ 2 /2.

Hexahedron Volume Formula

La formula per il volume di un esaedro regolare dei lati "a" è un ^ 3, dal momento che un esaedro regolare è un cubo.

L'area di superficie è, naturalmente, un ^ 2 --- 6 lati = 6a ^ 2.