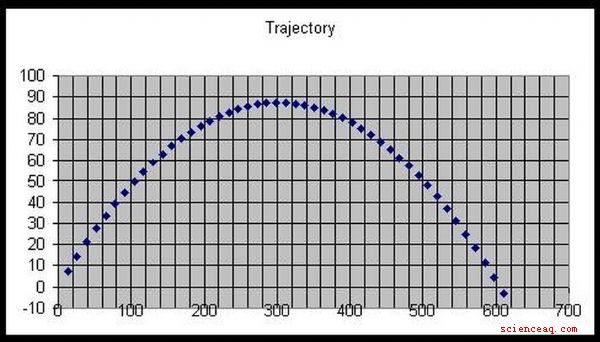
Ogni volta che un slugger lancia una palla fuori dal parco o un arciere lancia una freccia, l'oggetto che sfreccia nell'aria sta seguendo un percorso balistico, o traiettoria. Determinare e predire questa traiettoria richiede di rompere il problema nelle sue componenti orizzontali e verticali. In un percorso balistico, l'accelerazione è zero nella direzione orizzontale ed è uguale all'accelerazione della gravità nella direzione verticale. Poiché l'accelerazione è la seconda derivata dell'accelerazione, l'integrazione di questi valori produce per due volte le equazioni per la posizione.

Rompere la velocità iniziale nelle sue componenti verticali e orizzontali. Dovrai già conoscere l'angolo con cui è stato sparato l'oggetto e la sua velocità iniziale. Per questo esempio, un arciere lancia una freccia a 30 gradi con una velocità di 150 ft /sec. V0x = 150_cos (30) = 130 ft /sec V0y = 150_sin (30) = 75 ft /sec

Scegli un valore per il tempo e calcola la distanza orizzontale in quel momento. È meglio iniziare con zero e percorrere la traiettoria in modo incrementale. Per questo esempio, il valore viene calcolato in t = 1. x = V0x_t = 130_1 = 130 piedi

Calcola il valore per la distanza verticale nello stesso intervallo di tempo. Il valore per l'accelerazione gravitazionale nelle unità inglesi è 32.2 ft /sec ^ 2. y = V0y_t - 0.5_g_t ^ 2 = 75 (1) - 0.5_32.2 * 1 ^ 2 = 58.9 ft

Traccia i valori orizzontali e verticali su un foglio di carta millimetrata. Scegli un altro valore temporale e calcola un altro set di coordinate. Continua finché non hai abbastanza punti per definire la tua traiettoria.

Suggerimento

La posizione di y = 0 è ovunque l'oggetto abbia iniziato il volo libero, non necessariamente il terreno. Ciò significa che un oggetto può viaggiare sotto lo zero nella direzione verticale nella parte in basso della traiettoria.