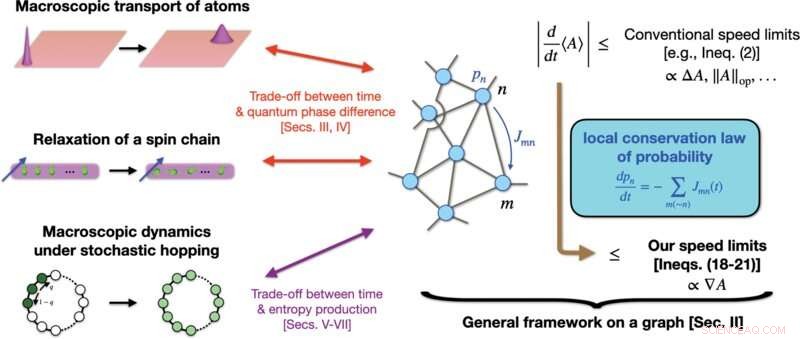
Illustrazione schematica delle nostre realizzazioni. Stabiliamo un quadro generale per derivare limiti di velocità qualitativamente più stretti di una quantità A rispetto a molti convenzionali, che dipendono dall'intera gamma di A , come ΔA o ∥A ∥op . La nostra strategia consiste nel mappare le dinamiche generali di nostro interesse alle dinamiche su un grafico, dove utilizziamo la conservazione locale della probabilità. In contrasto con i limiti convenzionali, i nostri limiti di velocità coinvolgono la pendenza ∇A di A sul grafico, che può stringere significativamente il limite quando ∇A ≪ΔA o ∥A ∥op . Quando applicata a sistemi quantistici macroscopici (come il trasporto macroscopico di atomi o il rilassamento di una catena di spin perturbata localmente), la nostra teoria indica una nuova relazione di compromesso tra il tempo e la differenza di fase quantistica. Quando applicata alla dinamica stocastica macroscopica, inclusa quella quantistica, la nostra teoria indica una relazione di compromesso tra tempo e quantità come la produzione di entropia. Credito:PRX Quantum (2022). DOI:10.1103/PRXQuantum.3.020319
Un fisico teorico della RIKEN ha ricavato un'espressione per la velocità massima alla quale possono verificarsi cambiamenti nei sistemi macroscopici. Ciò approfondirà la nostra comprensione dei fenomeni quantistici nei sistemi che non sono in equilibrio.
Uno degli aspetti più difficili da comprendere della meccanica quantistica è il principio di indeterminazione di Heisenberg che afferma che non è possibile definire contemporaneamente sia la posizione che la quantità di moto di un oggetto. In altre parole, più precisamente viene determinata la posizione di una particella, più ampio diventa l'intervallo della sua possibile quantità di moto (e viceversa).
Nel 1945, due fisici, Leonid Mandelstam e Igor Tamm, si concentrarono su un altro tipo di relazione di incertezza, vale a dire quella tra tempo e fluttuazione di energia, e mostrarono che le transizioni nei sistemi quantistici non avvengono istantaneamente; piuttosto, la velocità con cui si verifica una transizione è limitata da un importo determinato da quanto fluttua l'energia del sistema.
Successivamente sono stati derivati molti altri cosiddetti limiti di velocità quantistica, che hanno aiutato a comprendere meglio la fisica dei sistemi quantistici e sono stati utili in varie applicazioni quantistiche.
Ma grossi problemi sorgono quando i limiti di velocità quantistica vengono applicati ai sistemi macroscopici. "I precedenti limiti di velocità quantistica, che sono utili per piccoli sistemi, in genere diventano privi di significato per le transizioni macroscopiche", osserva Ryusuke Hamazaki del Nonequilibrium Quantum Statistical Mechanics RIKEN Hakubi Research Team. "Ad esempio, i limiti di velocità quantistici convenzionali danno un limite superiore infinito per la velocità delle transizioni in un gas composto da atomi."
Ora, Hamazaki è riuscito a derivare un limite di velocità quantistico per le transizioni nei sistemi macroscopici.
"Questa nuova derivazione fornisce limiti fondamentali che possono essere applicati a vari tipi di fenomeni macroscopici quantistici di non equilibrio", afferma. "Spero che molte leggi fondamentali e applicazioni riguardanti la dinamica quantistica macroscopica appaiano basate sui concetti introdotti in questo studio."
Hamazaki ha derivato il più rigoroso limite di velocità quantistica sviluppando un quadro generale basato sulla legge di conservazione della probabilità, un principio fondamentale in fisica.
Un risultato inaspettato per Hamazaki è stata la scoperta di una nuova relazione di scambio. "Invece di una relazione di compromesso tra tempo e fluttuazione di energia, come nel limite Mandelstam-Tamm, ne ho trovata una tra il tempo e il gradiente della fase quantistica, una quantità fondamentale nella fisica quantistica."
Hamazaki ora intende estendere la sua strategia per vedere se può essere utilizzata per derivare limiti di velocità quantistica per quantità come la crescita dell'entanglement quantistico. + Esplora ulteriormente