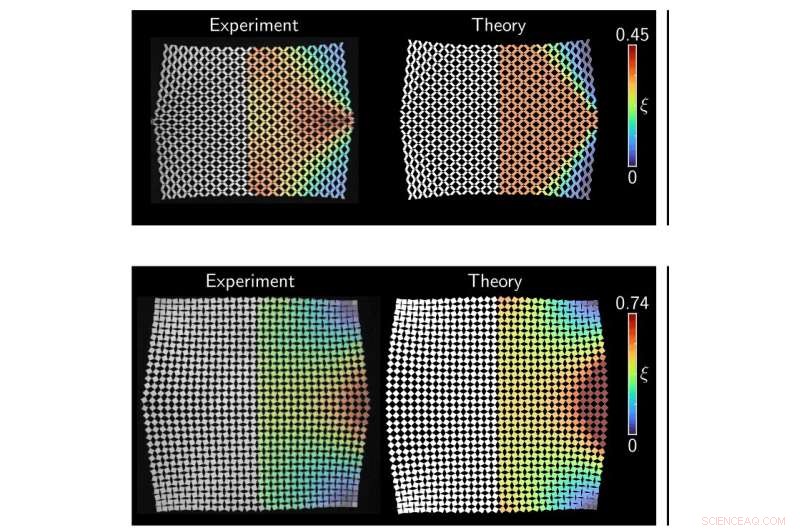
Due modelli cellulari 16 × 16 dopo la deformazione. La riga superiore è non auxetica (si contrae quando viene tirata) e iperbolica o ondulata. La riga inferiore è auxetica (si espande quando viene tirata) ed ellittica. Credito:Paul Plucinsky
Una gru di carta tradizionale è un'impresa artistica. Ogni piega nell'origami porta alla trasformazione di un singolo foglio di carta quadrato in un uccello, un drago o un fiore. L'origami sconsiglia di incollare, segnare o tagliare la carta, ma nell'arte del kirigami, i tagli posizionati strategicamente possono trasformare ulteriormente la forma della carta, creando strutture complesse da semplici fessure. Un noto esempio di questo è un libro pop-up, dove, a seconda di come viene tagliata la carta piatta, quando il libro viene aperto emergerà un diverso insieme di forme:un cuore, una rana, un insieme di grattacieli.
Nella produzione, il kirigami sta cambiando il gioco di ciò che è possibile. Proprio come con la carta, il taglio laser ripetuto di un foglio apre la possibilità di complesse trasformazioni di forme alimentate dall'apertura e dalla chiusura di fessure. Grazie alla libertà disponibile nella progettazione delle fessure, ciò crea un'ampia scelta di geometrie che hanno proprietà altamente adattabili rispetto ai materiali tradizionali. Nelle applicazioni del mondo reale, potresti vedere un tale materiale utilizzato nella robotica o nello spazio, ad esempio una pelle di serpente come materiale ispirato al kirigami che consente a un robot di gattonare o una cellula che si trasforma. Ma prima che questi materiali possano essere adattati per l'uso professionale, dobbiamo capire meglio come i materiali kirigami cambiano forma sotto carichi e sollecitazioni ingegneristiche tipiche. Sebbene le regole per i semplici elementi costitutivi siano note, le regole per le loro interazioni collettive di mutaforma rimangono in gran parte poco chiare.
In un recente articolo pubblicato in Physical Review Letters , un team interdisciplinare di ricercatori dell'USC, dell'Università dell'Illinois a Chicago e della Stony Brook University ha derivato una nuova equazione matematica per classificare il comportamento dei materiali ispirati al kirigami per prevedere meglio come si muoveranno quando vengono spinti o tirati. Il team comprende l'assistente professore dell'USC Paul Plucinsky e il collega post-dottorato Yue Zheng; Il professore associato della Stony Brook University Paolo Celli e l'assistente alla ricerca laureata Imtiar Niloy; e Ian Tobasco, Assistant Professor dell'Università dell'Illinois-Chicago.
Plucinsky ha detto:"La geometria di questi materiali è sintonizzata in modo alquanto arbitrario. Quindi abbiamo bisogno di regole su come scegliere le architetture che creerai. Una volta che hai queste regole, devi anche essere in grado di modellare il sistema in modo che fai qualche ragionevole previsione su come si deformerà quando viene spinto o tirato."
Plucinsky afferma che i precedenti modelli di comportamento dei materiali non si applicano ai materiali kirigami, poiché non sono sensibili alla complicata geometria dei loro progetti. "Se vuoi essere in grado di utilizzare questi materiali, devi prima capire perché quando introduci questi modelli ai carichi, producono una risposta molto non uniforme."
Quando un materiale viene tagliato, produce "celle" o spazi contenuti che si ripetono secondo uno schema, ad esempio parallelogrammi, ha detto Plucinsky. Nel caso dei materiali kirigami, queste celle possono essere classificate per comportarsi in due modi:ondulatorio o in decadimento lungo archi ellittici, e questo dipende solo dal fatto che il modello si comprima o si espanda perpendicolarmente alla direzione di trazione. Un'equazione matematica governa il comportamento geometrico di cose come il flusso d'acqua, ha detto Plucinsky, ma per solidi come questi è più difficile da derivare. Un'equazione differenziale parziale (PDE) è ciò che Plucinsky e il suo team sono stati in grado di sviluppare e presentare come il primo pezzo di un puzzle più grande necessario per rendere i materiali kirigami praticamente applicabili.
Un problema di modellazione
In questo momento, dice Plucinsky, mentre le persone sono ansiose di utilizzare materiali kirigami per progettare dispositivi nelle arene della robotica morbida, biomedica e persino della ricerca spaziale, c'è un problema di modellazione di base che ne impedisce l'uso. Plucinsky ha detto che non si sa molto su come funzionano i materiali kirigami in condizioni di carico di base. "Se non si dispone di un buon strumento per modellare i sistemi in questione, sarebbe difficile investigare lo spazio di progettazione e fare previsioni complete sui singoli modelli", ha affermato Plucinsky.
Alla luce di ciò, Plucinsky e il suo gruppo di ricerca hanno pensato, "esiste una semplice equazione matematica che potrebbe caratterizzare questi materiali?" "L'equazione", ha detto, "ti permetterebbe di prevedere il comportamento del sistema in modo numericamente efficiente ."
La chiave dell'equazione era rendersi conto che le celle di kirigami, pur avendo essi stessi complicati blocchi costitutivi, potevano essere concettualizzate come atomi in un reticolo (un insieme 2D ripetuto di atomi), come in un solido cristallino convenzionale, dove le unità sono identiche e si ripetono . Da lì, è stato semplice ricavare un'equazione che riuscisse a riflettere i cambiamenti nella struttura fisica di un tale materiale quando manipolato. L'equazione fornisce informazioni sugli scenari del mondo reale, ad esempio, come un oggetto spaziale basato su kirigami potrebbe reagire se una roccia lunare si posasse su di esso.
Puzzle di design
I modelli Kirigami, ha detto Plucinsky, sono utili per molte ragioni, una delle quali è che sono indipendenti dal materiale in molti modi. "Questo tipo di parallelismo è perfettamente in linea con la produzione additiva in cui ora possono praticamente entrare e su varie scale creare modelli accuratamente progettati. Il punto è che il modello è importante, quindi se si progetta il modello correttamente, la scelta del materiale che si utilizza non lo fa Non deve essere così importante."
Vedere il successo del modello matematico nella previsione dei materiali ispirati al kirigami apre le porte all'utilizzo di tale modellazione per altri materiali, ha affermato Plucinsky. "Stiamo lavorando verso l'idea che se hai qualcosa con uno schema ripetuto, puoi trovare un'equazione che lo modelli accuratamente. Da lì, possiamo capovolgerlo in modo che se vuoi progettare una proprietà particolare, può dire "oh, deve presentare un modello di tipo x" e decodificarlo". + Esplora ulteriormente