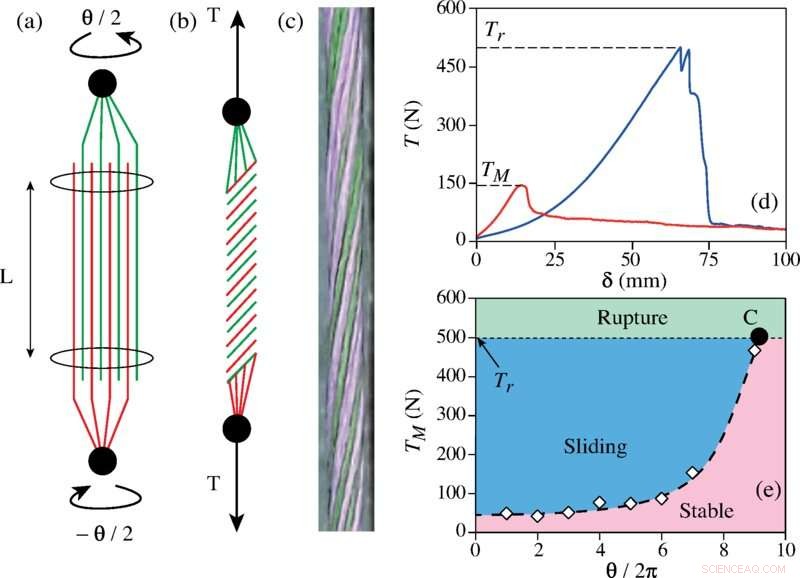
Credito:Lettere di revisione fisica (2022). DOI:10.1103/PhysRevLett.128.078002
Una coppia di ricercatori dell'Universit´e Paris-Saclay, CNRS e Univ Rennes, CNRS, IPR, rispettivamente, ha utilizzato la matematica per aiutare a descrivere il processo coinvolto quando fili corti di fibra vengono intrecciati in lunghi tratti di filato. Nel loro articolo pubblicato sulla rivista Physical Review Letters, Antoine Seguin e Jérôme Crassous descrivono come hanno utilizzato esperimenti e simulazioni per comprendere meglio i fattori coinvolti quando le fibre vengono attorcigliate insieme.
Gli esseri umani hanno attorcigliato insieme brevi fili di fibre per creare lunghi fili di corda o filato per migliaia di anni e, sebbene il processo generale sia ben compreso, la matematica dietro è stata piuttosto imprecisa. In questo nuovo sforzo, Seguin e Crassous hanno affrontato il problema utilizzando un nuovo approccio, applicando sia esperimenti che simulazioni.
Poiché diverse fibre corte sono attorcigliate insieme, si intrecciano, ma questo ovviamente non è sufficiente per tenerle insieme. Si tengono insieme a causa dell'attrito coinvolto. Tirare le estremità di un pezzo di filo costringe i singoli fili di cui è composto a spingersi l'uno nell'altro, aumentando la quantità di attrito e quindi la sua forza. Ma ci sono regole matematiche che governano il processo? Qual è il numero ottimale di fibre, ad esempio, per garantire il filato più resistente? Oppure quale grado di resistenza è dato al filo dal grado di attrito tra due fili di fibra?
Per trovare queste risposte, i ricercatori hanno condotto più test su diverse fibre intrecciate in filati. Hanno scoperto che un aumento delle torsioni aumenta la forza di legame delle fibre, ma solo fino a un certo punto. Inoltre, ogni tipo di fibra aveva il suo punto di rottura. Creando simulazioni per testare più facilmente diverse configurazioni, hanno anche scoperto che c'era un raggio di fibra ottimale per una data lunghezza di filo e che la forza del filo veniva scalata con l'esponenziale del quadrato dell'angolo di torsione.
Nella ricerca di elementi in comune, hanno scoperto quello che descrivono come il numero di torsione di Ercole, un parametro che descrive le forze coinvolte con l'angolo di torsione, un coefficiente di attrito e il raggio del filo. Hanno anche scoperto che questo numero in generale era proporzionale al quadrato del numero di torsioni applicate e aveva un valore critico di 30. Hanno anche sviluppato una formula per mostrare la dimensione ottimale del raggio per un determinato tipo di fibra. + Esplora ulteriormente
© 2022 Rete Science X