Le reti possono rappresentare sistemi in cambiamento, come la diffusione di un’epidemia o la crescita di gruppi in una popolazione di persone. Ma anche la struttura di queste reti può cambiare, man mano che i collegamenti compaiono o svaniscono nel tempo. Per comprendere meglio questi cambiamenti, i ricercatori spesso studiano una serie di "istantanee" statiche che catturano la struttura della rete in un breve periodo.

I teorici della rete hanno cercato modi per combinare queste istantanee. In un nuovo articolo in Physical Review Letters , un trio di ricercatori affiliati allo SFI descrive un nuovo modo per aggregare istantanee statiche in cluster più piccoli di reti preservando al tempo stesso la natura dinamica del sistema. Il loro metodo, ispirato a un'idea della meccanica quantistica, prevede il test di coppie successive di istantanee di rete per trovare quelle per le quali una combinazione comporterebbe l'effetto più piccolo sulla dinamica del sistema, e quindi combinarle.

È importante sottolineare che può determinare come semplificare il più possibile la storia della struttura della rete mantenendo la precisione. I calcoli alla base del metodo sono abbastanza semplici, afferma l'autore principale Andrea Allen, ora data scientist presso il Children's Hospital di Filadelfia.

"Siamo davvero entusiasti di poterlo condividere, ed è sorprendente che nessun altro abbia pubblicato esattamente questa idea negli ultimi dieci anni", afferma Allen. Ha collaborato con il professor Cris Moore, fisico e matematico della SFI, e Laurent Hébert-Dufresne, scienziato della complessità presso l'Università del Vermont ed ex membro della SFI James S. McDonnell Foundation.

Nell'articolo pubblicato il metodo non appare complicato; in realtà, si è evoluto nel corso degli anni sia all'interno che all'esterno dello SFI. La collaborazione è iniziata nel 2015 quando Allen, allora studente universitario in matematica, ha visitato lo SFI per un mese in inverno e poi, nell'estate del 2016, è tornato per partecipare al programma Research Experiences for Undergraduates (ora chiamato Undergraduate Complexity Research program). .

Hébert-Dufresne aveva ottenuto un ampio set di dati, acquisito dai dati del telefono satellitare, che utilizzava i "ping" dei telefoni cellulari per mostrare come le persone si muovevano. Era interessato a trovare comunità, ma voleva anche essere in grado di misurare se comunità diverse richiedevano risoluzioni dei dati diverse.

"Ad esempio, i sistemi di sorveglianza epidemica dovrebbero essere uniformi tra le comunità quando sappiamo che comunità diverse hanno comportamenti diversi?"

Quella domanda ha portato a qualcosa di più:"A quale livello possiamo aggregare tutto ciò pur mantenendo le differenze? E come facciamo a saperlo?" chiede Allen. "Non vogliamo perdere l'integrità della rete che stiamo cercando di studiare."

Hanno coinvolto Moore per fare un brainstorming di idee su come sapere quali differenze erano importanti per la struttura complessiva e quali erano meno importanti. Poi dopo un po' hanno accantonato il progetto.

Allen lasciò il mondo accademico per diventare uno sviluppatore di software e Hébert-Dufresne fondò il suo gruppo di ricerca nel Vermont. Ma sarebbe una pausa breve. Due anni dopo, Allen si unì al gruppo di Hébert-Dufresne nel Vermont come studente laureato e ripresero da dove avevano interrotto.

"Abbiamo sempre detto:'concludiamo questa cosa adesso'", dice Allen. "Questa cosa è diventata una specie di scherzo per otto anni."

Nella fase finale, i ricercatori hanno identificato un modo semplice per approssimare l’errore e per utilizzarlo in combinazioni successive di coppie di reti. Nell'articolo, i ricercatori utilizzano la diffusione della malattia come metro di misura per valutare e convalidare il metodo.

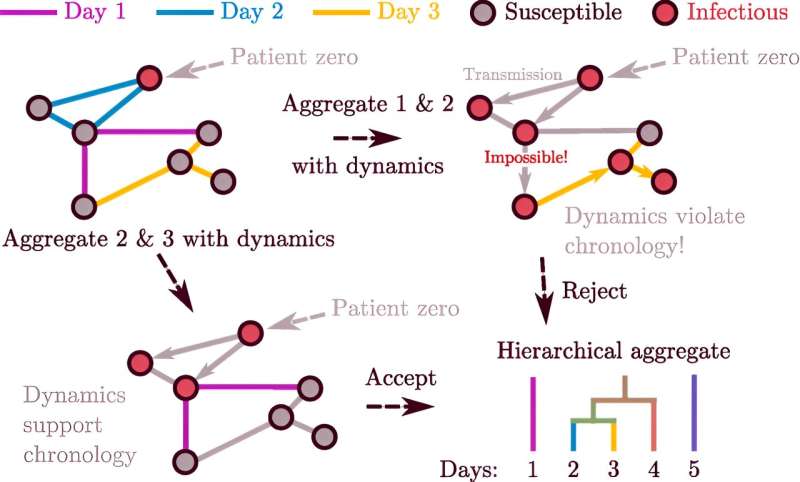
"Supponiamo che ci sia una pandemia", dice Moore. Se due persone – Alice e Bob – si uniscono, e poi altre due persone – diciamo Bob e Charlene – si uniscono, allora la malattia potrebbe diffondersi da Alice a Charlene ma non il contrario. L'ordine di questi collegamenti è importante, il che significa che è fuorviante combinarli in un'unica istantanea (e trattarli come se fossero simultanei).

Il nuovo metodo prende in prestito un’idea dalla meccanica quantistica per identificare questo tipo di errori. In quel campo, il “commutatore” può rivelare quanto conta l’ordine nei calcoli che coinvolgono cose come l’energia e la quantità di moto. Nella nuova applicazione, i ricercatori hanno utilizzato un commutatore per decidere quanto conta l'ordine e quando è corretto combinare le istantanee.

"Questo ci consente di semplificare il più possibile la storia della struttura della rete mantenendo la precisione", afferma Moore. Indica inoltre un modo per addomesticare un set di dati enorme e ingombrante in un insieme di reti più piccolo e gestibile.

Allen afferma che potrebbe essere esteso ad altri sistemi dinamici come la diffusione di informazioni su una rete di social media.

Ulteriori informazioni: Andrea J. Allen et al, Compressione della cronologia di una rete temporale con commutatori di grafici, Lettere di revisione fisica (2024). DOI:10.1103/PhysRevLett.132.077402

Fornito da Santa Fe Institute