La maggior parte del calcolo nelle reti neurali all'avanguardia comprende operazioni lineari, ad esempio moltiplicazioni e convoluzioni di matrici-vettori. Anche le operazioni lineari possono svolgere un ruolo importante nella crittografia. Sebbene siano disponibili processori dedicati come GPU e TPU per eseguire operazioni lineari altamente parallele, questi dispositivi sono assetati di energia e la ridotta larghezza di banda dell'elettronica limita ancora la loro velocità operativa. L'ottica è più adatta per tali operazioni grazie al suo parallelismo intrinseco, all'ampia larghezza di banda e alla velocità di calcolo.
Costruite da una serie di superfici sottili progettate spazialmente, reti neurali profonde diffrattive (D 2 NN), note anche come reti diffrattive, formano un'architettura di calcolo ottico emergente in grado di eseguire attività computazionali passivamente alla velocità di propagazione della luce attraverso un volume ultrasottile.
Questi computer completamente ottici specifici per attività sono progettati digitalmente attraverso l'apprendimento delle caratteristiche spaziali delle loro superfici diffrattive costituenti. Dopo questo processo di progettazione una tantum, le superfici ottimizzate vengono fabbricate e assemblate per formare l'hardware fisico della rete ottica diffrattiva.
Nella loro pubblicazione su Advanced Photonics Nexus , un team di ricercatori guidato da Aydogan Ozcan, professore del rettore e cattedra Volgenau per l'innovazione ingegneristica presso l'UCLA, ha introdotto un metodo per eseguire operazioni lineari a valori complessi con reti diffrattive sotto illuminazione spazialmente incoerente.
In precedenza era stato dimostrato dallo stesso gruppo che le reti diffrattive con sufficienti gradi di libertà possono eseguire trasformazioni lineari arbitrarie con valori complessi con luce spazialmente coerente con errore trascurabile.
Al contrario, con la luce spazialmente incoerente, queste reti possono eseguire trasformazioni lineari arbitrarie delle intensità ottiche in ingresso se gli elementi della matrice che definiscono la trasformazione sono reali e non negativi. Dato che le fonti di illuminazione spazialmente incoerenti sono più diffuse e di più facile accesso, c'è una crescente necessità di processori diffrattivi spazialmente incoerenti per gestire i dati oltre i semplici valori non negativi.
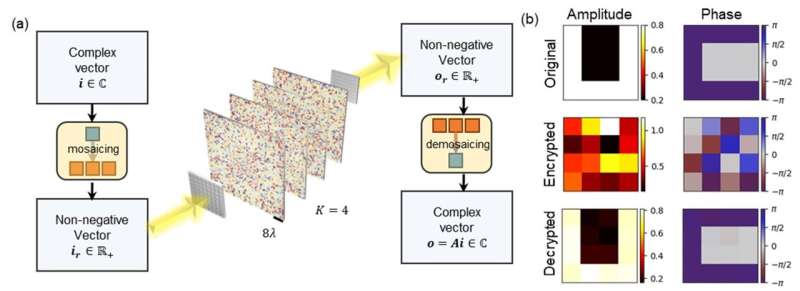
Incorporando fasi di preelaborazione e postelaborazione per rappresentare i numeri complessi mediante un insieme di numeri reali non negativi, i ricercatori dell'UCLA hanno esteso la potenza di elaborazione delle reti diffrattive spazialmente incoerenti al dominio dei numeri complessi.
Hanno dimostrato che tali processori diffrattivi incoerenti possono essere progettati per eseguire una trasformazione lineare arbitraria di valori complessi con errore trascurabile se è presente un numero sufficiente di caratteristiche diffrattive di sola fase ottimizzabili all'interno del progetto, che si adatta alle dimensioni del complesso di input e output spazi vettoriali.
I ricercatori hanno mostrato l'applicazione di questo nuovo schema tramite crittografia e decrittografia di immagini con valori complessi utilizzando reti diffrattive spazialmente incoerenti. Oltre alla crittografia delle immagini visive, tali processori diffrattivi spazialmente incoerenti potrebbero essere utili anche in altre applicazioni, ad esempio nei veicoli autonomi per l'elaborazione ultraveloce e a basso consumo di scene naturali.
Ulteriori informazioni: Xilin Yang et al, Trasformazioni lineari universali a valori complessi e crittografia delle immagini utilizzando reti diffrattive spazialmente incoerenti, Advanced Photonics Nexus (2024). DOI:10.1117/1.APN.3.1.016010
Fornito da UCLA Engineering Institute for Technology Advancement