I ricercatori dell'Università di Ottawa (uOttawa), in collaborazione con il Weizmann Institute of Science e la Lancaster University, hanno osservato una transizione quantistica nascosta che può essere vista solo a seconda di come gli osservatori eseguono le misurazioni.
Lo studio "Transizioni topologiche della fase Pancharatnam-Berry generalizzata" è stato pubblicato su Science Advances il 24 novembre 2023.
Una parte essenziale del metodo scientifico si basa sulla capacità di misurare accuratamente il risultato di un esperimento e di giustapporre questi risultati con risultati precedenti. Gli scienziati sviluppano dispositivi di misurazione, o misuratori, che consentono loro di quantificare con precisione l'entità delle proprietà fisiche. Tuttavia, il "processo di misurazione" solleva una domanda critica e intrigante:il processo di misurazione di un parametro altera il sistema misurato?
In fisica si ritiene spesso che l’influenza sul sistema sia trascurabile. Tuttavia, lo stesso presupposto non può essere fatto nel contesto della meccanica quantistica, poiché l'atto di misurazione può avere un impatto significativo sul sistema sotto osservazione.
Il gruppo di ricerca, guidato da Yuval Gefen, professore della Facoltà di Fisica presso il Weizmann Institute of Science e Ebrahim Karimi, professore di fisica e Canada Research Chair in Structured Quantum Waves presso la Facoltà di Scienze dell'Università di Ottawa, ha ideato un sofisticato protocollo per osservare questa transizione topologica guidata dalla misurazione.
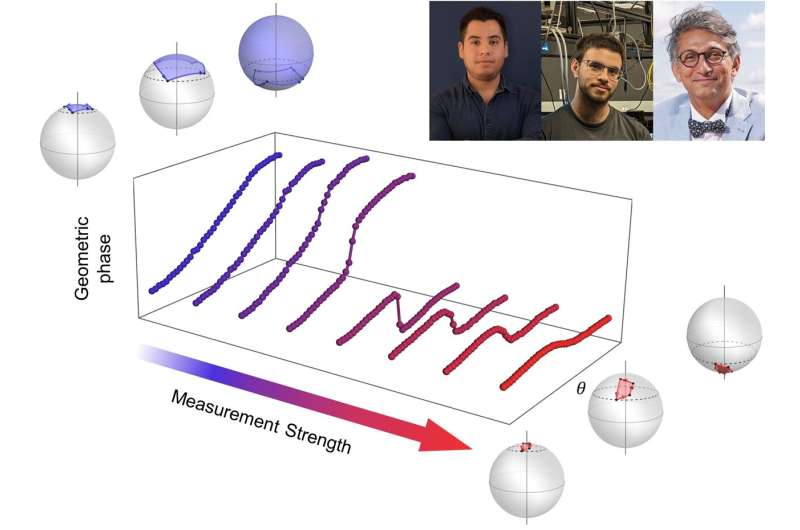
Questo protocollo prevedeva una sequenza ciclica di misurazioni con intensità variabili, da forte a debole, sullo stato di polarizzazione dei fotoni emessi da una sorgente laser. I loro risultati rivelano che mentre la transizione topologica rimane intatta nonostante la presenza di imperfezioni sia nel sistema che nel processo, è anche sensibile a queste imperfezioni.
"Questa sensibilità si manifesta in alterazioni significative nella posizione e nella forma della transizione, sottolineando il delicato equilibrio tra l'integrità del sistema e le influenze esterne in esplorazioni scientifiche così avanzate", ha affermato Manuel F. Ferrer-Garcia, Ph.D. candidato, che ha condotto l'esperimento di laboratorio presso il Nexus for Quantum Technologies Institute di uOttawa.
Nella meccanica quantistica, è ampiamente accettato che l'intero stato di un sistema quantistico sia incapsulato nella sua funzione d'onda. Per conoscere lo stato, il sistema interagisce con un dispositivo di misurazione, ovvero i contatori, che sono strumentali per quantificare la grandezza di una proprietà fisica. Convenzionalmente, gli scienziati quantistici utilizzano una tecnica nota come misurazioni proiettive nel loro laboratorio.
Queste misurazioni sono considerate "forti" poiché provocano il "collasso" della funzione d'onda, dove viene ridotta ad uno stato specifico allineato con uno degli stati del dispositivo di misurazione. Questo processo non solo produce informazioni ma altera anche lo stato quantistico iniziale del sistema. Tuttavia, è possibile ideare un protocollo di misurazione che influenzi minimamente il sistema, portando a letture alquanto indeterminate sul nostro misuratore.
Attraverso interazioni ripetute, diventa possibile raccogliere informazioni sul sistema, un processo chiamato misurazioni "deboli". Da questa comprensione, possiamo dedurre il potenziale per la progettazione di protocolli di misurazione il cui impatto varia tra questi due estremi:forte e debole. Questo concetto apre nuove strade per esplorare i sistemi quantistici e le loro interazioni con i dispositivi di misurazione, segnando un passo avanti significativo nelle tecniche di misurazione quantistica.
Un aspetto significativo ma meno evidente dei fenomeni quantistici è la loro profonda connessione con i concetti topologici. La topologia, in sostanza, è una branca della matematica focalizzata sullo studio delle proprietà che sono invarianti o cambiano in modo discontinuo sotto deformazioni continue. Un esempio di questi invarianti è il numero di fori nelle superfici chiuse:ad esempio, una sfera può essere trasformata continuamente in una forma a ciambella, ma il numero di fori cambierà bruscamente da zero a uno quando due diversi punti della superficie entrano in contatto tra loro. .
Gli invarianti topologici svolgono un ruolo importante in molte aree della fisica moderna. In questo lavoro, i ricercatori hanno osservato una transizione topologica quando la forza di misurazione cambia da forte a debole. Questa transizione ha coinvolto il comportamento di un altro concetto matematico:la fase geometrica o Pancharatnam-Berry.
Quando uno stato quantistico subisce un'evoluzione ciclica, cioè ritorna allo stato iniziale dopo un certo periodo di tempo, può acquisire una fase "globale", dovuta unicamente alla curvatura dello spazio in cui avviene l'evoluzione. Questa fase può essere osservata interferendo lo stato evoluto con quello iniziale.
L’impatto di questa ricerca va oltre l’ambito della fisica fondamentale. Poiché la transizione si è rivelata sensibile a determinate caratteristiche del sistema quantistico, ha il potenziale per essere utilizzata in applicazioni di rilevamento o caratterizzazione di elementi ottici.
Ulteriori informazioni: Manuel F. Ferrer-Garcia et al, Transizioni topologiche della fase Pancharatnam-Berry generalizzata, Progressi scientifici (2023). DOI:10.1126/sciadv.adg6810
Informazioni sul giornale: La scienza avanza
Fornito dall'Università di Ottawa