Questo articolo mostrerà come disegnare i grafici della funzione radice quadrata usando solo tre valori diversi per 'x', quindi trovando i punti attraverso i quali viene disegnato il grafico delle equazioni /funzioni, mostrerà anche come i grafici Traslazione verticale (sposta verso l'alto o verso il basso), Trasla orizzontalmente (si sposta a sinistra oa destra) e come il grafico fa entrambe le traduzioni.
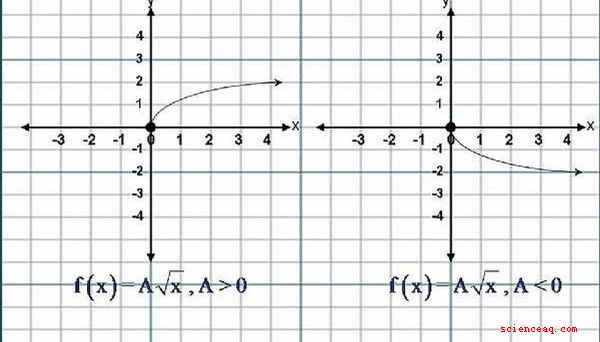
L'equazione di una funzione di radice quadrata ha la forma, .. . y = f (x) = A√x, dove (A) non deve essere uguale a zero (0). Se (A) è maggiore di Zero (0), cioè (A) è un numero positivo, quindi The La forma del grafico della radice quadrata La funzione è simile alla metà superiore della lettera, 'C'. Se (A) è minore di zero (0), ovvero (A) è un numero negativo, la forma del grafico è simile a quella della metà inferiore della lettera "C". Clicca sull'immagine per una migliore visualizzazione.
Per tracciare il grafico dell'equazione, ... y = f (x) = A√x, scegliamo Tre valori per 'x', x = ( -1), x = (0) e x = (1). Sostituiamo ogni valore di 'x' nell'Equazione, ... y = f (x) = A√x e otteniamo il rispettivo valore corrispondente per ogni 'y'.
Dato y = f (x) = A√x, dove (A) è un numero reale e (A) non uguale a zero (0), e sostituendo, x = (-1) nell'equazione otteniamo y = f (-1) = A√ ( -1) = i (che è un numero immaginario). Quindi il primo punto non ha coordinate reali, quindi non è possibile tracciare un grafico attraverso questo punto. Ora Sostituendo, x = (0), otteniamo y = f (0) = A√ (0) = A (0) = 0. Quindi il Secondo Punto ha Coordinate (0,0). E Sostituendo x = (1) otteniamo y = f (1) = A√ (1) = A (1) = A. Quindi il Terzo Punto ha le Coordinate (1, A). Poiché il primo punto aveva coordinate che non erano reali, ora cerchiamo un quarto punto e scegliamo x = (2). Ora sostituisci x = (2) in y = f (2) = A√ (2) = A (1.41) = 1.41A. Quindi il quarto punto ha coordinate (2,1.41A). Ora disegniamo la curva attraverso questi tre punti. Clicca sull'immagine per una migliore visualizzazione.
Data l'equazione y = f (x) = A√x + B, dove B è un numero reale, il grafico di questa equazione si tradurrebbe verticalmente (B) unità. Se (B) è un numero positivo, il grafico si muoverà verso l'alto (B) unità, e se (B) è un numero negativo, il grafico si sposterà verso il basso (B) unità. Per disegnare i grafici di questa equazione, seguiamo le istruzioni e usiamo gli stessi valori di "x" del punto # 3. Clicca sull'immagine per avere una vista migliore.
Data l'equazione y = f (x) = A√ (x - B) dove A e B sono numeri reali, e (A) non è uguale a Zero (0) e x ≥ B. Il grafico di questa equazione dovrebbe tradurre le unità orizzontali (B). Se (B) è un numero positivo, il grafico si sposterà sulle unità di destra (B) e se (B) è un numero negativo, il grafico si sposterà sulle unità di sinistra (B). Per disegnare i grafici di questa equazione, per prima cosa impostiamo l'espressione 'x-B', cioè sotto il segno radicale Maggiore o uguale a zero, e risolviamo con 'x'. Cioè, ... x - B ≥ 0, quindi x ≥ B.
Ora utilizzeremo i seguenti tre valori per 'x', x = (B), x = (B + 1) e x = (B + 2). Sostituiamo ogni valore di 'x' nell'Equazione, ... y = f (x) = A√ (x - B) e otteniamo il rispettivo valore corrispondente per ogni 'y'.
Dato y = f (x) = A√ (x - B), dove A e B sono numeri reali e (A) non uguale a Zero (o) dove x ≥ B. Sostituendo, x = (B) nell'equazione otteniamo = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Quindi il primo punto ha le coordinate (B, 0). Ora Sostituendo, x = (B + 1), otteniamo y = f (B + 1) = A√ (B + 1 - B) = A√1 = A (1) = A. Quindi il Secondo Punto ha Coordinate ( B + 1, A), e Sostituendo x = (B + 2) otteniamo y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1.41) = 1.41A . Quindi il terzo punto ha coordinate (B + 2,1,41 A). Ora disegniamo la curva attraverso questi tre punti. Clicca sull'immagine per una migliore visualizzazione.
Dato y = f (x) = A√ (x - B) + C, dove A, B, C sono numeri reali e (A) non uguale a Zero (0) e x ≥ B. Se C è un numero positivo, il grafico in STEP # 7 tradurrà le unità verticalmente (C). Se (C) è un numero positivo, il grafico si muoverà verso l'alto (C), e se (C) è un numero negativo, il grafico si sposterà verso il basso (C). Per tracciare i grafici di questa equazione, seguiamo le istruzioni e usiamo gli stessi valori di "x" del punto # 7. Clicca sull'immagine per avere una visione migliore.