La cronologia di solito inizia all'inizio del tempo e poi collega eventi evolutivi al presente in modo da poter capire come sei arrivato dove sei. Con la matematica, in questo caso gli esponenti, avrà molto più senso iniziare con una comprensione e un significato attuali di esponenti e lavorare a ritroso da dove sono venuti. Prima di tutto, assicuriamoci di capire cosa sia un esponente perché può diventare piuttosto complicato. In questo caso, lo terremo tutto semplice.
Dove siamo adesso
Questa è la versione per liceo, quindi dovremmo capirlo tutti. Un esponente riflette un numero moltiplicato per se stesso, come 2 volte 2 uguale a 4. In forma esponenziale che potrebbe essere scritto 2², chiamato due al quadrato. Il 2 sollevato è l'esponente e il minuscolo 2 è il numero base. Se si desidera scrivere 2x2x2, potrebbe essere scritto come 2 o 2 alla terza potenza. Lo stesso vale per qualsiasi numero base, 8² è 8x8 o 64. Lo capisci. Puoi usare qualsiasi numero come base e il numero di volte che vuoi moltiplicarlo da solo diventerebbe l'esponente.
Da dove venivano gli esponenti?
La parola stessa deriva dal latino, expo, che significa fuori, e ponere, che significa luogo. Mentre la parola esponente arrivò a significare cose diverse, il primo uso moderno registrato dell'esponente in matematica era in un libro intitolato "Arithemetica Integra", scritto nel 1544 dall'autore e matematico inglese Michael Stifel. Ma stava lavorando semplicemente con una base di due, quindi l'esponente 3 significherebbe il numero di 2 che avresti bisogno di moltiplicare per ottenere 8. Assomiglierebbe a questo 2³ = 8. Il modo in cui afferma Stifel è un po 'arretrato rispetto al modo in cui lo pensiamo oggi. Diceva "3 è il 'partire' di 8". Oggi faremo riferimento all'equazione semplicemente come 2 cubetti. Ricorda, stava lavorando esclusivamente con una base o fattore 2 e traducendo dal latino un po 'più letteralmente di quanto facciamo oggi.
Occorrenze precedenti apparenti
Sebbene non sia sicuro al cento per cento, sembra che l'idea di quadratura o cubatura risale ai tempi babilonesi. Babilonia faceva parte della Mesopotamia nella zona che ora considereremmo l'Iraq. La prima menzione conosciuta di Babilonia si trova su una tavoletta risalente al XXIII secolo aC. E anche allora si stavano facendo strada con il concetto di esponenti, anche se il loro sistema di numerazione (sumerico, ora una lingua morta) utilizza i simboli per abbassare le formule matematiche. Stranamente, non sapevano cosa fare con il numero 0, quindi è stato delineato da uno spazio tra i simboli.
Come apparivano i primi esponenti
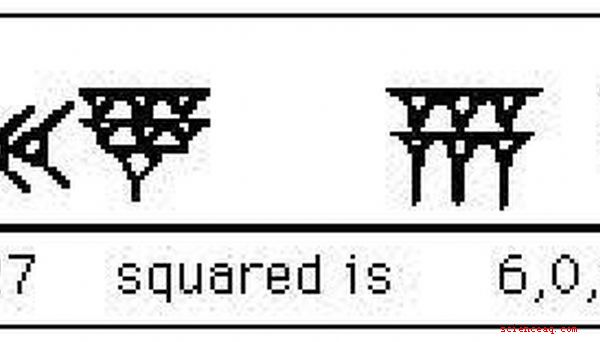
Il sistema di numerazione era ovviamente diverso dalla matematica moderna. Senza entrare nel dettaglio di come e perché era diverso, basti dire che avrebbero scritto il quadrato di 147 in questo modo. Nel sistema sessagesimale della matematica, che è quello che usavano i babilonesi, il numero 147 sarebbe stato scritto 2,27. La quadratura produrrebbe nei giorni moderni, il numero di telefono 21.609. In Babilonia è stato scritto 6,0,9. In sessagesimale 147 = 2,27 e quadratura dà il numero 21609 = 6,0,9. Questo è quello che sembrava l'equazione, come scoperto su un'altra tavoletta antica. (Prova a inserirlo nella calcolatrice).
Perché esponenti?
Che cosa succede se, ad esempio, in una formula matematica complessa, devi calcolare qualcosa di veramente importante. Potrebbe essere qualsiasi cosa e ha richiesto di sapere cosa 9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9x9 uguale. E c'erano molti numeri così grandi nell'equazione. Non sarebbe molto più semplice scrivere 9³³? Puoi capire che numero è se ti interessa. In altre parole è una scorciatoia, proprio come molti altri simboli in matematica sono abbreviati, che denotano altri significati e permettono di scrivere formule complesse in un modo più conciso e comprensibile. Un avvertimento da tenere a mente. Qualsiasi numero elevato a zero è uguale a 1. Questa è una storia per un altro giorno.