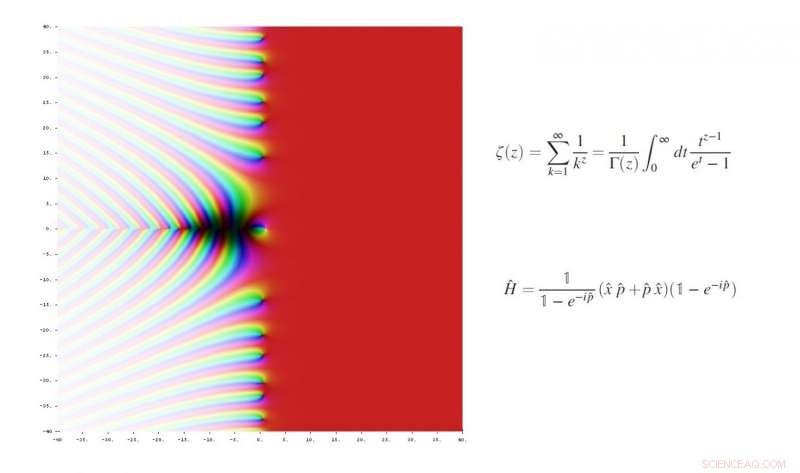
Nel 1859, Riemann ipotizzò che gli zeri non banali della funzione zeta di Riemann giacciano sulla retta verticale (½ + it) sul piano complesso, in cui la parte reale è sempre ½. Credito:Jan Homann, Wikimedia Commons. In alto:funzione zeta di Riemann. In basso:la nuova funzione operatore.
(Phys.org)—I ricercatori hanno scoperto che le soluzioni di una famosa funzione matematica chiamata funzione zeta di Riemann corrispondono alle soluzioni di un'altra, diverso tipo di funzione che può rendere più facile risolvere uno dei più grandi problemi in matematica:l'ipotesi di Riemann. Se i risultati possono essere rigorosamente verificati, allora dimostrerebbe finalmente l'ipotesi di Riemann, che vale $ 1, 000, 000 Millennium Prize del Clay Mathematics Institute.
Mentre l'ipotesi di Riemann risale al 1859, negli ultimi 100 anni circa i matematici hanno cercato di trovare una funzione di operatore come quella scoperta qui, in quanto è considerato un passaggio chiave nella dimostrazione.
"Per quello che ci risulta, questa è la prima volta che è stato identificato un operatore esplicito - e forse sorprendentemente relativamente semplice - i cui autovalori ['soluzioni' nella terminologia matriciale] corrispondono esattamente agli zeri non banali della funzione zeta di Riemann, "Dorje Brody, un fisico matematico della Brunel University di Londra e coautore del nuovo studio, detto Phys.org .
Quello che resta ancora da dimostrare è il secondo passaggio chiave:che tutti gli autovalori sono numeri reali piuttosto che immaginari. Se il lavoro futuro può dimostrarlo, allora dimostrerebbe finalmente l'ipotesi di Riemann.
Brody e i suoi coautori, i fisici matematici Carl Bender della Washington University di St. Louis e Markus Müller della University of Western Ontario, hanno pubblicato il loro lavoro in un recente numero di Lettere di revisione fisica .
Spaziatura dei numeri primi
L'ipotesi di Riemann ha un fascino così forte perché è profondamente connessa alla teoria dei numeri e, in particolare, i numeri primi. Nel suo articolo del 1859, Il matematico tedesco Bernhard Riemann ha studiato la distribuzione dei numeri primi, o più precisamente, il problema "dato un intero N, quanti sono i numeri primi minori di N?"
Riemann ipotizzò che la distribuzione dei numeri primi minori di N sia correlata agli zeri non banali di quella che ora viene chiamata funzione zeta di Riemann, ( S ). (Gli zeri sono le soluzioni, o i valori di S che rendono la funzione uguale a zero. Sebbene fosse facile per i matematici vedere che ci sono zeri ogni volta che... S è un numero pari negativo, questi zeri sono considerati zeri banali e non sono la parte interessante della funzione.)
L'ipotesi di Riemann era che tutti gli zeri non banali giacciono lungo una singola linea verticale (½ + esso ) nel piano complesso, il che significa che la loro componente reale è sempre ½, mentre la loro componente immaginaria io varia man mano che si sale e si scende lungo la linea.
Negli ultimi 150 anni, i matematici hanno trovato letteralmente trilioni di zeri non banali, e tutti hanno una componente reale di ½, proprio come pensava Riemann. È opinione diffusa che l'ipotesi di Riemann sia vera, e molto lavoro è stato fatto sulla base di questo presupposto. Ma nonostante gli sforzi intensi, l'ipotesi di Riemann - che tutti gli infiniti zeri giacciono su questa singola linea - non è stata ancora dimostrata.
Soluzioni identiche
Uno degli indizi più utili per dimostrare l'ipotesi di Riemann è venuto dalla teoria delle funzioni, che rivela che i valori della parte immaginaria, T , in cui la funzione si annulla sono numeri discreti. Ciò suggerisce che gli zeri non banali formano un insieme di numeri reali e discreti, che è proprio come gli autovalori di un'altra funzione chiamata operatore differenziale, che è ampiamente usato in fisica.
Agli inizi del 1900, questa somiglianza ha portato alcuni matematici a chiedersi se esista davvero un operatore differenziale i cui autovalori corrispondono esattamente agli zeri non banali della funzione zeta di Riemann. Oggi questa idea è chiamata congettura di Hilbert-Pólya, prende il nome da David Hilbert e George Pólya, nonostante il fatto che nessuno dei due abbia pubblicato nulla al riguardo.
"Poiché non esiste alcuna pubblicazione di Hilbert o Pólya, l'esatta affermazione del programma Hilbert-Pólya è soggetta in una certa misura all'interpretazione, ma probabilmente non è irragionevole dire che consiste di due passaggi:(a) trovare un operatore i cui autovalori corrispondono agli zeri non banali della funzione zeta di Riemann; e (b) determinare se gli autovalori sono reali, " ha detto Brody.
"Finora l'obiettivo principale del nostro lavoro è stato il passaggio (a), " ha detto. "Abbiamo identificato un operatore i cui autovalori corrispondono esattamente agli zeri non banali della funzione zeta di Riemann. Stiamo solo iniziando a pensare al passaggio (b), e in effetti come affrontare questa sfida. Se sarà difficile o facile completare i passaggi mancanti verso il passaggio (b), a questo punto non possiamo speculare:è necessario ulteriore lavoro per avere un'idea migliore dell'entità delle difficoltà coinvolte".
L'operatore
Una delle cose interessanti dell'operatore appena scoperto è che ha stretti legami con la fisica quantistica.
Nel 1999, quando i fisici matematici Michael Berry e Jonathan Keating stavano studiando la congettura di Hilbert-Pólya, fecero un'altra importante congettura. Se esiste un tale operatore, loro hanno detto, allora dovrebbe corrispondere ad un sistema quantistico teorico con particolari proprietà. Questa è ora chiamata congettura di Berry-Keating. Ma nessuno ha mai trovato un sistema del genere prima d'ora, e questo è un secondo aspetto importante del nuovo lavoro.
"Abbiamo identificato una condizione di quantizzazione per l'hamiltoniana di Berry-Keating, verificando così sostanzialmente la validità della congettura di Berry-Keating, " ha detto Brody.
Le Hamiltoniane sono spesso usate per descrivere l'energia dei sistemi fisici. Il nuovo operatore, però, non sembra descrivere alcun sistema fisico, ma è piuttosto una funzione puramente matematica.
"Potrebbe essere deludente, ma un tale Hamiltoniano non sembra rappresentare sistemi fisici in alcun modo ovvio; o almeno finora non abbiamo trovato alcuna indicazione che la nostra Hamiltoniana corrisponda a qualsiasi sistema fisico, " ha detto Brody.
"Ma ci si potrebbe chiedere 'perché pubblicare in? PRL ?' La risposta è perché molte delle tecniche utilizzate per alcune analisi euristiche nel nostro articolo che sono suggestive sono prese in prestito da tecniche di teoria quantistica pseudo-hermitiana PT-simmetrica sviluppate negli ultimi 15 anni circa. La comprensione convenzionale della congettura di Hilbert-Pólya è che l'operatore (Hamiltoniano) dovrebbe essere hermitiano, e si collega naturalmente questo alla teoria dei quanti, per la quale si pretende convenzionalmente che le Hamiltoniane siano hermitiane. Proponiamo una forma pseudo-hermitiana del programma Hilbert-Pólya, che a noi sembra utile approfondire."
Soluzioni reali
Ora la sfida più grande che rimane è dimostrare che gli autovalori dell'operatore sono numeri reali.
Generalmente, i ricercatori sono ottimisti sul fatto che gli autovalori siano effettivamente reali, e nel loro articolo presentano un forte argomento per questo basato sulla simmetria PT, un concetto della fisica quantistica. Fondamentalmente, La simmetria PT dice che puoi cambiare i segni di tutte e quattro le componenti dello spazio-tempo (tre dimensioni spaziali o di "parità" e una dimensione temporale), e, se il sistema è PT-simmetrico, quindi il risultato sarà lo stesso dell'originale.
Sebbene la natura in generale non sia PT-simmetrica, l'operatore che i fisici hanno costruito è. Ma ora i ricercatori vogliono dimostrare che questa simmetria si rompe. Come spiegano nel loro articolo, se si può dimostrare che la simmetria PT è rotta per la parte immaginaria dell'operatore, allora ne seguirebbe che gli autovalori sono tutti numeri reali, che costituirebbe finalmente la tanto attesa prova dell'ipotesi di Riemann.
Si ritiene generalmente che una dimostrazione dell'ipotesi di Riemann sarà molto utile in informatica, soprattutto la crittografia. I ricercatori vogliono anche determinare cosa potrebbero effettivamente significare i loro risultati per comprendere i principi matematici più fondamentali.
"Ciò che abbiamo esplorato finora contiene poche intuizioni di teoria dei numeri; mentre ci si potrebbe aspettare che, data la sua importanza nella teoria dei numeri, sicuramente qualsiasi tentativo che faccia progressi con successo nello stabilire l'ipotesi di Riemann offrirebbe intuizioni sulla teoria dei numeri, " disse Brody. "Naturalmente questo non deve essere affatto il caso, ma nondimeno sarebbe interessante esplorare se qualcuno degli aspetti dinamici dell'ipotetico sistema descritto dal nostro Hamiltoniano possa essere collegato a certi risultati della teoria dei numeri. A questo proposito, l'analisi semi-classica sulla nostra Hamiltoniana sarebbe uno dei prossimi obiettivi".
© 2017 Phys.org