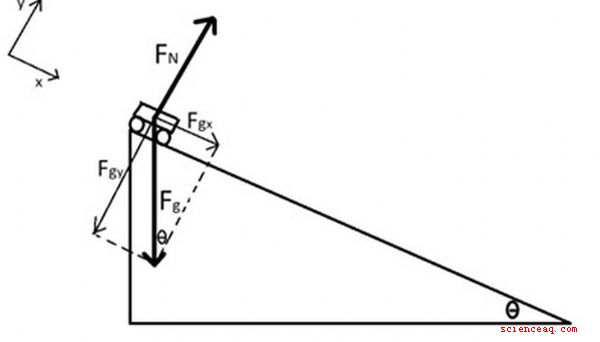
La forza netta
è la somma vettoriale di tutte le forze che agiscono su un corpo. (Ricorda che una forza è una spinta o una trazione.) L'unità SI per la forza è il newton (N), dove 1 N \u003d 1 kgm /s ^{2.
\\ bold {F_ {net}} \u003d \\ bold {F_1 + F_2 + F_3 + ...}}

La prima legge di Newton afferma che un oggetto sottoposto a moto uniforme - ovvero che è a riposo o che si muove a velocità costante - continuerà a farlo a meno che non venga agito da una rete diversa da zero vigore. La seconda legge di Newton ci dice esplicitamente come il movimento cambierà a seguito di questa forza netta:
\\ bold {F_ {net}} \u003d m \\ bold {a}

L'accelerazione - variazione di velocità nel tempo - è direttamente proporzionale alla forza netta. Si noti inoltre che sia l'accelerazione che la forza netta sono quantità vettoriali che puntano nella stessa direzione.

TL; DR (troppo lungo; non letto)

Una forza netta di zero NON necessariamente significa che l'oggetto è fermo! Una forza netta di zero NON significa anche che non vi siano forze che agiscono su un oggetto in quanto è possibile che forze multiple agiscano in modo tale da annullarsi a vicenda.
Diagrammi del corpo libero

Il primo passo per trovare la forza netta su qualsiasi oggetto è disegnare un diagramma a corpo libero
(FBD) che mostra tutte le forze che agiscono su quell'oggetto. Questo viene fatto rappresentando ogni vettore di forza come una freccia proveniente dal centro dell'oggetto e indicando nella direzione in cui agisce la forza.

Ad esempio, supponiamo che un libro sia seduto su un tavolo. Le forze che agiscono su di esso sarebbero la forza di gravità sul libro, che agisce verso il basso, e la forza normale del tavolo sul libro, che agisce verso l'alto. Il diagramma del corpo libero di questo scenario consisterebbe in due frecce di uguale lunghezza originate dal centro del libro, una rivolta verso l'alto e l'altra rivolta verso il basso.

(immagine 1)

Supponiamo lo stesso libro veniva spinto a destra con una forza di 5 N mentre una forza di attrito 3-N si opponeva al movimento. Ora il diagramma del corpo libero includerebbe una freccia 5-N a destra e una freccia 3-N a sinistra.

(immagine 2)

Infine, supponiamo che lo stesso libro fosse su un'inclinazione, che scende. In questo scenario, le tre forze sono la forza gravitazionale sul libro, che punta verso il basso; la forza normale sul libro, che punta perpendicolarmente alla superficie; e la forza di attrito, che punta in senso opposto alla direzione del movimento.

(immagine 3)
Calcolo della forza netta

Dopo aver disegnato il diagramma del corpo libero, puoi usare l'aggiunta vettoriale per trovare la forza netta che agisce sull'oggetto. Prenderemo in considerazione tre casi mentre esploriamo questa idea:

Caso 1: tutte le forze si trovano sulla stessa linea.

Se tutte le forze si trovano sulla stessa linea (puntando solo a sinistra e a destra o solo su e giù, per esempio), determinare la forza netta è semplice come aggiungere le magnitudini delle forze nella direzione positiva e sottrarre le magnitudini delle forze nella direzione negativa. (Se due forze sono uguali e opposte, come nel caso del libro appoggiato sul tavolo, la forza netta \u003d 0)

Esempio: si consideri una palla da 1 kg che cade a causa della gravità, sperimentando una resistenza dell'aria forza di 5 N. C'è una forza verso il basso a causa della gravità di 1 kg × 9,8 m /s ^{2 \u003d 9,8 N e una forza verso l'alto di 5 N. Se usiamo la convenzione che su è positivo, allora la forza netta è 5 N - 9,8 N \u003d -4,8 N, che indica una forza netta di 4,8 N nella direzione verso il basso.}

(immagine 4)

Caso 2: tutte le forze giacciono su perpendicolare assi e aggiungi a 0 lungo un asse.

In questo caso, a causa delle forze che si aggiungono a 0 in una direzione, dobbiamo solo concentrarci sulla direzione perpendicolare durante la determinazione della forza netta. (Sebbene la consapevolezza che le forze nella prima direzione si aggiungano a 0 a volte può darci informazioni sulle forze nella direzione perpendicolare, ad esempio quando si determinano le forze di attrito in termini di grandezza della forza normale.)

Esempio: A La macchinina da 0,25 kg viene spinta sul pavimento con una forza di 3 N che agisce a destra. Una forza di attrito 2-N agisce per contrastare questo movimento. Si noti che la gravità agisce anche verso il basso su questa vettura con una forza di 0,25 kg × 9,8 m /s ^{2 \u003d 2,45 N, e una forza normale agisce verso l'alto, anche con 2,45 N. (Come facciamo a saperlo? Poiché non vi è alcun cambiamento nel movimento nella direzione verticale mentre la macchina viene spinta sul pavimento, quindi la forza netta nella direzione verticale deve essere 0.)
Questo semplifica tutto nel caso monodimensionale perché le uniche forze che non si annullano sono tutti in una direzione. La forza netta sull'auto è quindi 3 N - 2 N \u003d 1 N a destra.}

(immagine 5)

Caso 3: tutte le forze non sono confinate su una linea e non giacere su assi perpendicolari.

Se sappiamo in quale direzione si troverà l'accelerazione, sceglieremo un sistema di coordinate in cui tale direzione si trova sull'asse x positivo o sull'asse y positivo. Da lì, spezziamo ogni vettore di forza in componenti x e y. Poiché il movimento in una direzione è costante, la somma delle forze in quella direzione deve essere 0. Le forze nell'altra direzione sono quindi gli unici contribuenti alla forza netta e questo caso si è ridotto a Caso 2.

Se non sappiamo in quale direzione andrà l'accelerazione, possiamo scegliere qualsiasi sistema di coordinate cartesiane, sebbene di solito sia più conveniente sceglierne una in cui una o più forze si trovino su un asse. Suddividere ciascun vettore di forza in componenti X e Y. Determinare la forza netta nella direzione x
e la forza netta nella direzione y
separatamente. Il risultato fornisce le coordinate x e y della forza netta.

Esempio: un'auto da 0,25 kg rotola senza attrito lungo un'inclinazione di 30 gradi a causa della gravità.

Useremo un sistema di coordinate allineato con la rampa come mostrato. Il diagramma del corpo libero è costituito dalla gravità che agisce verso il basso e dalla forza normale che agisce perpendicolarmente alla superficie.

Dobbiamo suddividere la forza gravitazionale in componenti x e y, che fornisce:
F_ { gx} \u003d F_g \\ sin (\\ theta) \\\\ F_ {gy} \u003d F_g \\ cos (\\ theta)

Poiché il movimento nella direzione y
è costante, sappiamo che la forza netta nella y
la direzione deve essere 0:
F_N - F_ {gy} \u003d 0

(Nota: questa equazione ci consente di determinare l'entità della forza normale.)

Nella direzione x, l'unica forza è F _{gx
, quindi:
F_ {net} \u003d F_ {gx} \u003d F_g \\ sin (\\ theta) \u003d mg \\ sin (\\ theta) \u003d 0.25 \\ times9.8 \\ times \\ sin (30) \u003d 1.23 \\ text {N} Come trovare l'accelerazione dalla forza netta}

Dopo aver determinato il vettore della forza netta, trovare il l'accelerazione di un oggetto è una semplice applicazione della seconda legge di Newton.
\\ bold {F_ {net}} \u003d m \\ bold {a} \\ implica \\ bold {a} \u003d \\ frac {\\ bold {F_ {net}} } {m}

Nell'esempio precedente dell'auto da 0,25 kg che rotola giù rampa, la forza netta era 1,23 N lungo la rampa, quindi l'accelerazione sarebbe:
\\ bold {a} \u003d \\ frac {\\ bold {F_ {net}}} {m} \u003d \\ frac {1.23} {0.25 } \u003d 4.92 \\ text {m /s} ^ 2 \\ text {giù per la rampa}