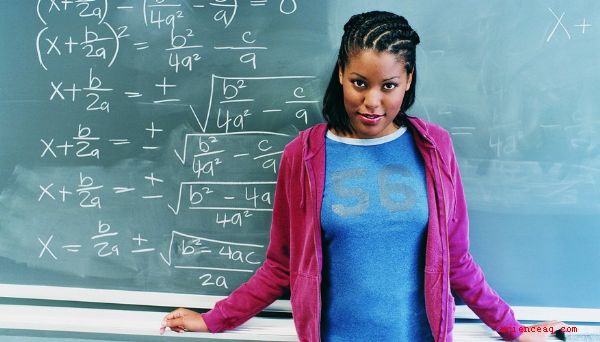
Per molti studenti, le equazioni quadratiche di factoring tendono ad essere tra gli aspetti più impegnativi di un corso di algebra delle superiori o dei college. Il processo implica una grande quantità di conoscenza dei prerequisiti, come la familiarità con la terminologia algebrica e la capacità di risolvere equazioni lineari a più fasi. Esistono diversi metodi per risolvere le equazioni quadratiche - le più comuni delle quali sono il factoring, il grafico e la formula quadratica - e le domande che dovresti porti variano in base al metodo che usi.
Uguale a Zero

Indipendentemente dal metodo che stai utilizzando, devi prima chiederti se l'equazione quadratica è impostata uguale a zero. Matematicamente parlando, l'equazione deve essere nella forma ax ^ 2 + bx + c \u003d 0, dove "a", "b" e "c" sono numeri interi e "a" non è uguale a zero. (Vedi riferimento 1 o riferimento 2) A volte le equazioni possono già essere presentate in quella forma, ad esempio 3x ^ 2 - x - 10 \u003d 0. Tuttavia, se entrambi i lati del segno uguale includono termini diversi da zero, è necessario aggiungere o sottrai i termini da una parte per spostarli dall'altra parte. Ad esempio, in 3x ^ 2 - x - 4 \u003d 6, prima di risolvere è necessario sottrarre sei da entrambi i lati dell'equazione, per ottenere 3x ^ 2 - x - 10 \u003d 0.
Factoring

Se stai considerando questo metodo, prima chiediti se il coefficiente del termine quadrato, "a", è qualcosa di diverso da uno. Se lo è, come nel caso di 3x ^ 2 - x - 10 \u003d 0, dove "a" è tre, prendere in considerazione l'uso di un altro metodo, poiché probabilmente sarà molto più veloce del factoring. Altrimenti, il factoring può essere un metodo rapido ed efficace. Durante il factoring, chiediti se i numeri che hai inserito tra parentesi si moltiplicano per produrre "c" e aggiungi per produrre "b". Ad esempio, se risolvendo x ^ 2 - 5x - 36 \u003d 0, hai scritto (x - 9) (x + 4) \u003d 0, sei sulla strada giusta perché -9 * 4 \u003d -36 e -9 + 4 \u003d -5.
Grafica

Prima di iniziare questo metodo, assicurati di avere una calcolatrice grafica. In caso contrario, selezionare un altro metodo, poiché la rappresentazione grafica a mano sarà ingombrante. Dopo aver inserito l'equazione e ottenuto il grafico, chiediti se la dimensione della finestra di visualizzazione ti consente di trovare la soluzione. Graficamente, le soluzioni per un'equazione quadratica sono costituite dai valori x dei punti in cui la parabola attraversa l'asse x. A seconda dell'equazione particolare, se la finestra di visualizzazione è troppo piccola, potresti non essere in grado di vedere questi punti. Ad esempio, in x ^ 2 - 11x - 26 \u003d 0, è immediatamente evidente che una delle soluzioni è x \u003d -2, ma la seconda soluzione probabilmente non è visibile perché è un numero maggiore delle impostazioni standard della finestra nella maggior parte calcolatrici grafiche. Per trovare la seconda soluzione, aumentare i valori x nelle impostazioni della finestra fino a quando non è visibile; in questo esempio, aumenta il valore massimo finché non vedi che la parabola attraversa l'asse x con x \u003d 13.
Formula quadratica

Il metodo della formula quadratica può essere un metodo efficace perché funziona per risolvere qualsiasi equazione quadratica, compresi quelli con radici irrazionali o immaginarie. La formula quadratica è: x \u003d [-b più o meno la radice quadrata di (b ^ 2 - 4ac)] /(2a)]. Quando inserisci valori nella formula quadratica, chiediti se hai identificato correttamente "a", "b" e "c". Ad esempio, in 8x ^ 2 - 22x - 6 \u003d 0, a \u003d 8, b \u003d -22 e c \u003d -6. Chiediti anche se "b" è negativo - in tal caso, sarà positivo nella prima porzione della formula quadratica. Trascurare di invertire il segno di "b" in questo caso è un errore comune che molti studenti fanno. Ad esempio, l'esempio produce [22 più o meno la radice quadrata di (-22 ^ 2 - 4_8_-6) /(2 * 8)]. Semplifica con cura i termini, chiedendoti se stai gestendo correttamente i numeri negativi e applicando l'ordine delle operazioni. Se segui l'esempio, dovresti ottenere x \u003d 3 e x \u003d -0,25.