La tangente è una delle tre funzioni trigonometriche di base, le altre due sono seno e coseno. Queste funzioni sono essenziali per lo studio dei triangoli e mettono in relazione gli angoli del triangolo ai suoi lati. La definizione più semplice della tangente utilizza i rapporti dei lati di un triangolo rettangolo, e i metodi moderni esprimono questa funzione come la somma di una serie infinita. Le tangenti possono essere calcolate direttamente quando sono note le lunghezze dei lati del triangolo rettangolo e possono anche essere derivate da altre funzioni trigonometriche.
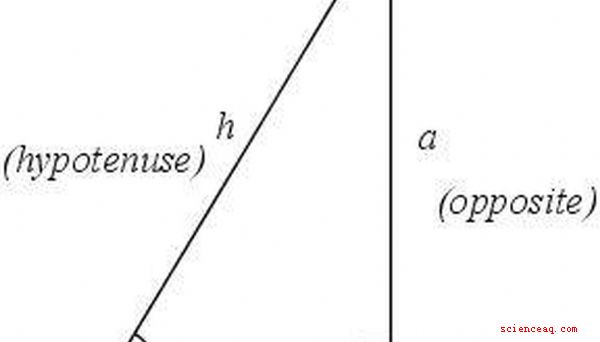
Identifica ed etichetta le parti di un triangolo rettangolo. L'angolo retto sarà al vertice C e il lato opposto sarà l'ipotenusa h. L'angolo &# x3B8; sarà al vertice A, e il restante vertice sarà B. Il lato adiacente all'angolo &# x3B8; sarà il lato b e il lato opposto all'angolo &# x3B8; sarà lato a. I due lati di un triangolo che non sono l'ipotenusa sono noti come le gambe del triangolo.
Definisce la tangente. La tangente di un angolo è definita come il rapporto tra la lunghezza del lato opposto all'angolo e la lunghezza del lato adiacente all'angolo. Nel caso del triangolo al passaggio 1, tan &# x3B8; \u003d a /b.
Determina la tangente per un triangolo rettangolo semplice. Ad esempio, le gambe di un triangolo rettangolo isoscele sono uguali, quindi a /b \u003d tan &# x3B8; \u003d 1. Anche gli angoli sono uguali, quindi &# x3B8; \u003d 45 gradi. Pertanto, tan 45 gradi \u003d 1.
Deriva la tangente dalle altre funzioni trigonometriche. Dal momento che seno &# x3B8; \u003d a /he coseno &# x3B8; \u003d b /h, quindi sinusoidale &# x3B8; /cosine &# x3B8; \u003d (a /h) /(b /h) \u003d a /b \u003d tan &# x3B8 ;. Pertanto, tan &# x3B8; \u003d seno &# x3B8; /cosine &# x3B8 ;.
Calcola la tangente per qualsiasi angolo e precisione desiderata:
sin x \u003d x - x ^ 3/3! + x ^ 5/5! - x ^ 7/7! + ... coseno x \u003d 1 - x ^ 2/2! + x ^ 4/4! - x ^ 6/6! + ... So tan x \u003d (x - x ^ 3/3! + X ^ 5/5! - x ^ 7/7! + ...) /(1 - x ^ 2/2! + X ^ 4 /4! - x ^ 6/6! + ...)