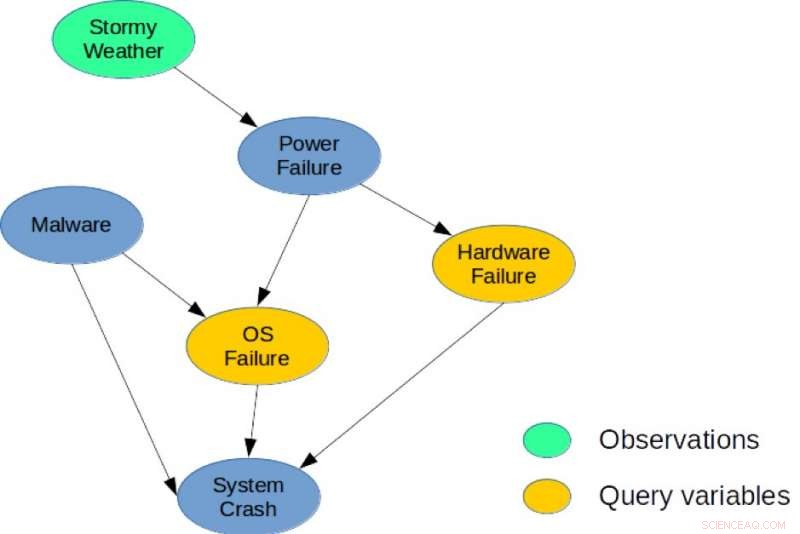
Figura 1. Una semplice rete bayesiana per un'attività di diagnosi del sistema. Credito:IBM
C'è una profonda connessione tra pianificazione e inferenza, e nell'ultimo decennio, più ricercatori hanno introdotto riduzioni esplicite che mostrano come la pianificazione stocastica può essere risolta utilizzando l'inferenza probabilistica con applicazioni in robotica, pianificazione, e problemi ambientali. Però, i metodi euristici e la ricerca sono ancora gli approcci più performanti per la pianificazione in ampi stati combinatori e spazi di azione. I miei coautori e io adottiamo un nuovo approccio nel nostro articolo, "Dalla pianificazione stocastica alla mappa marginale" (autori:Hao Cui, Radu Marinescu, Roni Khardon), alla Conferenza 2018 sui sistemi di elaborazione delle informazioni neurali (NeurIPS) mostrando come le idee della pianificazione possono essere utilizzate per l'inferenza.
Abbiamo sviluppato il Risolutore Algebrico Gradient-Based (AGS), un nuovo solutore per l'inferenza MAP marginale approssimata. L'algoritmo costruisce un grafico di calcolo algebrico approssimativo catturando i margini delle variabili di stato e ricompensa sotto ipotesi di indipendenza. Quindi utilizza la differenziazione automatica e la ricerca basata sul gradiente per ottimizzare la scelta dell'azione. La nostra analisi mostra che il valore calcolato dal grafico di calcolo AGS è identico alla soluzione di Belief Propagation (BP) quando è condizionato dalle azioni. Ciò fornisce una connessione esplicita tra algoritmi di pianificazione euristica e inferenza approssimata.
Più specificamente, rivisitiamo la connessione tra pianificazione stocastica e inferenza probabilistica. Proponiamo per la prima volta di utilizzare un algoritmo euristico efficiente che è stato originariamente progettato per risolvere problemi di pianificazione per affrontare un compito di inferenza centrale per modelli grafici probabilistici, vale a dire il compito di probabilità a posteriori massima marginale (MMAP).
I modelli grafici probabilistici come le reti bayesiane o le reti di Markov forniscono una struttura molto potente per ragionare sulle strutture di dipendenza condizionale su molte variabili. Per tali modelli, la query di inferenza MMAP è un compito particolarmente difficile ma importante, corrispondente a trovare la configurazione più probabile (o massimizzare la probabilità) su un sottoinsieme di variabili, chiamate variabili MAP, dopo aver marginalizzato (o sommato) il resto del modello.
L'inferenza MMAP si presenta in molte situazioni, soprattutto nelle attività di diagnosi e pianificazione, in cui la specificazione più naturale del modello contiene molte variabili i cui valori non ci interessa prevedere, ma che creano interdipendenza tra le variabili di interesse. Per esempio, in un compito di diagnosi basato su modelli, date osservazioni, cerchiamo di ottimizzare su un sottoinsieme di variabili di diagnosi che rappresentano componenti potenzialmente guasti in un sistema.
Per illustrazione, si consideri la rete bayesiana mostrata in Figura 1, che descrive un semplice problema di diagnosi per un sistema informatico. Il modello cattura le dipendenze causali dirette tra sei variabili casuali utilizzate per descrivere questo problema. Nello specifico, un arresto anomalo del sistema può essere causato da un guasto hardware, un guasto del sistema operativo, o la presenza di malware nel sistema. Allo stesso modo, un'interruzione dell'alimentazione potrebbe essere una causa comune di guasto dell'hardware e del sistema operativo, e Stormy Weather può causare l'interruzione di corrente. Una possibile query MMAP sarebbe quella di calcolare la configurazione più probabile di guasti hardware e sistema operativo, dato che osserviamo Stormy Weather, indipendentemente dallo stato delle altre variabili (Malware, arresto anomalo del sistema, o interruzione di corrente).
I quadri di pianificazione stocastici come i processi decisionali di Markov sono ampiamente utilizzati per modellare e risolvere compiti di pianificazione in condizioni di incertezza. La pianificazione a orizzonte finito può essere acquisita utilizzando una rete bayesiana dinamica (DBN) in cui le variabili di stato e di azione in ogni fase temporale sono rappresentate esplicitamente e le distribuzioni di probabilità condizionate delle variabili sono date dalle probabilità di transizione. Nella pianificazione off-line, il compito è quello di calcolare una politica che ottimizzi la ricompensa a lungo termine. In contrasto, nella pianificazione on-line ci viene dato un tempo limitato fisso t per passo e non possiamo calcolare una polizza in anticipo. Anziché, visto lo stato attuale, l'algoritmo deve decidere l'azione successiva entro il tempo t. Quindi l'azione viene eseguita, si osservano una transizione e una ricompensa e all'algoritmo viene presentato lo stato successivo. Questo processo si ripete e vengono valutate le prestazioni a lungo termine dell'algoritmo.
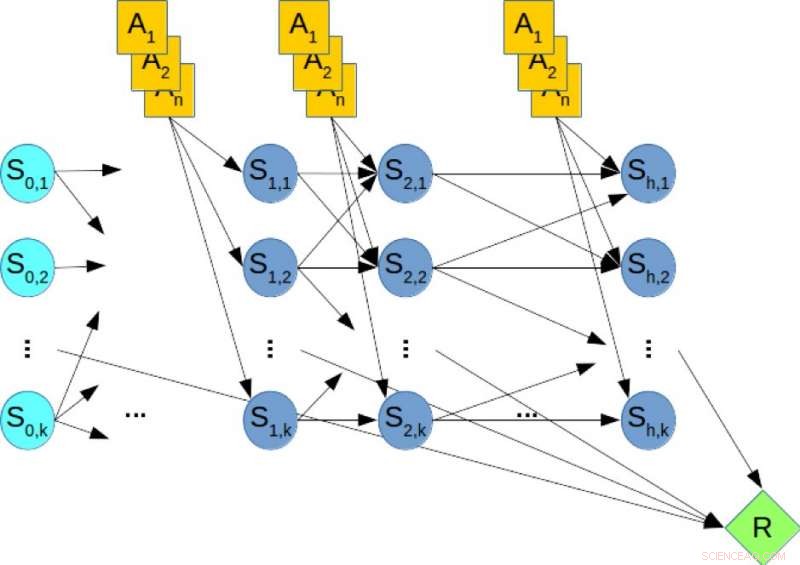
Figura 2. Una rete bayesiana dinamica (DBN) per la pianificazione stocastica. Credito:IBM
Per illustrazione, considera la Figura 2, che mostra il DBN corrispondente ad un ipotetico problema di pianificazione, dove i nodi arancioni rappresentano le variabili di azione, i nodi blu indicano le variabili di stato, e il nodo verde indica la ricompensa cumulativa che deve essere massimizzata. Perciò, calcolare la politica ottimale del problema di pianificazione equivale a risolvere una query MMAP sul DBN, dove massimizziamo le variabili di azione e marginalizziamo le variabili di stato.
La nostra valutazione sperimentale di istanze di problemi MMAP difficili mostra in modo conclusivo che lo schema AGS migliora le prestazioni in qualsiasi momento di algoritmi all'avanguardia su problemi MMAP con sottoproblemi di somma difficile, a volte fino a un ordine di grandezza. Riteniamo che queste connessioni tra pianificazione e inferenza possano essere ulteriormente esplorate per produrre miglioramenti in entrambi i campi.
Questa storia è stata ripubblicata per gentile concessione di IBM Research. Leggi la storia originale qui.