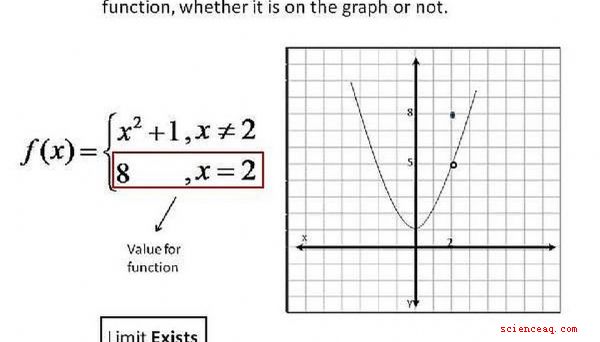
Useremo alcuni esempi di funzioni e i loro grafici per mostrare come possiamo determinare se il limite esiste quando x si avvicina a un determinato numero.

Ci sono quattro modi diversi per determinare se esiste un limite guardando il grafico per la funzione. Il primo, che mostra che il limite esiste, è se il grafico ha un buco nella linea, con un punto per quel valore di x su un valore diverso di y. Se ciò accade, allora il limite esiste, sebbene abbia un valore diverso per la funzione rispetto al valore per il limite. Per favore, clicca sull'immagine per una migliore comprensione.

Se c'è un buco nel grafico al valore a cui si sta avvicinando x, con nessun altro punto per un diverso valore della funzione, allora il limite esiste ancora . Si prega di vedere il grafico per una migliore comprensione.

Se il grafico ha un asintoto verticale, cioè due linee che si avvicinano al valore del limite che continua verso l'alto o verso il basso senza limiti, il limite non esiste. Fare clic sull'immagine per una migliore comprensione.

Se il grafico si avvicina a due numeri diversi da due direzioni diverse, poiché x si avvicina a un numero particolare, il limite non esiste. Non può essere due numeri diversi. Clicca sull'immagine per una migliore comprensione.