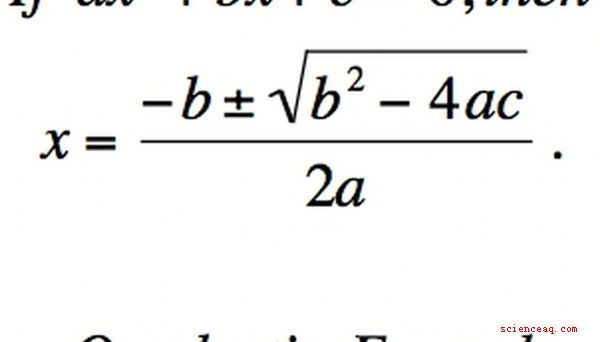
Il factoring di un polinomio si riferisce alla ricerca di polinomi di ordine inferiore (il più alto esponente è inferiore) che, moltiplicato insieme, produce il polinomio fattorizzato. Ad esempio, x ^ 2 - 1 può essere fattorizzato in x - 1 e x + 1. Quando questi fattori vengono moltiplicati, il -1x e + 1x si cancellano, lasciando x ^ 2 e 1.

Of Limited Power

Sfortunatamente, il factoring non è uno strumento potente, che limita il suo utilizzo nella vita quotidiana e nei campi tecnici. I polinomi sono pesantemente truccati nelle scuole elementari in modo che possano essere presi in considerazione. Nella vita di tutti i giorni, i polinomi non sono così amichevoli e richiedono strumenti di analisi più sofisticati. Un polinomio semplice come x ^ 2 + 1 non è fattorizzabile senza usare numeri complessi - cioè, numeri che includono i = √ (-1). I polinomi di ordine fino a 3 possono essere proibitivamente difficili da considerare. Ad esempio, x ^ 3 - y ^ 3 fa riferimento a (x - y) (x ^ 2 + xy + y ^ 2), ma non influisce ulteriormente senza ricorrere a numeri complessi.

Scienza delle scuole superiori

I polinomi del secondo ordine - ad es. x ^ 2 + 5x + 4 - sono presi regolarmente in considerazione nelle classi di algebra, circa l'ottavo o il nono grado. Lo scopo del factoring di tali funzioni è quello di essere in grado di risolvere equazioni di polinomi. Ad esempio, la soluzione per x ^ 2 + 5x + 4 = 0 sono le radici di x ^ 2 + 5x + 4, vale a dire, -1 e -4. Essere in grado di trovare le radici di tali polinomi è fondamentale per risolvere i problemi nelle lezioni di scienze nei seguenti 2 o 3 anni. Le formule del secondo ordine si presentano regolarmente in tali classi, ad esempio nei problemi del proiettile e nei calcoli di equilibrio acido-base.

La formula quadratica

Nel venire con strumenti migliori per sostituire il factoring, devi ricorda quale sia lo scopo del factoring in primo luogo: risolvere le equazioni. La formula quadratica è un modo per aggirare la difficoltà di prendere in considerazione alcuni polinomi mentre serve ancora lo scopo di risolvere un'equazione. Per le equazioni dei polinomi del secondo ordine (cioè, della forma ax ^ 2 + bx + c), la formula quadratica viene utilizzata per trovare le radici del polinomio e quindi la soluzione dell'equazione. La formula quadratica è x = [-b +/- √ (b ^ 2 - 4ac)] /[2a], dove +/- significa "più o meno". Si noti che non è necessario scrivere (x - root1) (x - root2) = 0. Invece di eseguire il factoring per risolvere l'equazione, la soluzione della formula può essere risolta direttamente senza factoring come passaggio intermedio, sebbene il metodo sia basato su fattorizzazione.

Questo non vuol dire che il factoring sia superfluo. Se gli studenti imparassero l'equazione quadratica di risolvere equazioni di polinomi senza imparare il factoring, la comprensione dell'equazione quadratica sarebbe ridotta.

Esempi

Questo non vuol dire che la fattorizzazione di polinomi non venga mai eseguita al di fuori di lezioni di algebra, fisica e chimica. I calcolatori finanziari palmari eseguono un calcolo degli interessi giornalieri utilizzando una formula che è la fattorizzazione dei pagamenti futuri con la componente interessi retrocessa (vedi diagramma). Nelle equazioni differenziali (equazioni dei tassi di cambiamento), la fattorizzazione di polinomi di derivati ​​(tassi di cambiamento) viene eseguita per risolvere quelle che vengono chiamate "equazioni omogenee di ordine arbitrario". Un altro esempio è nel calcolo introduttivo, nel metodo delle frazioni parziali per rendere più semplice l'integrazione (soluzione per l'area sotto una curva).

Soluzioni computazionali e uso dell'apprendimento in background

Questi esempi sono , ovviamente, lontano dalla quotidianità. E quando il factoring diventa difficile, abbiamo calcolatori e computer per fare il sollevamento pesi. Invece di prevedere una corrispondenza uno-a-uno tra ogni argomento matematico insegnato e calcoli quotidiani, guarda la preparazione che l'argomento fornisce per uno studio più pratico. Il factoring dovrebbe essere apprezzato per quello che è: un trampolino di lancio verso metodi di apprendimento per risolvere equazioni sempre più realistiche.