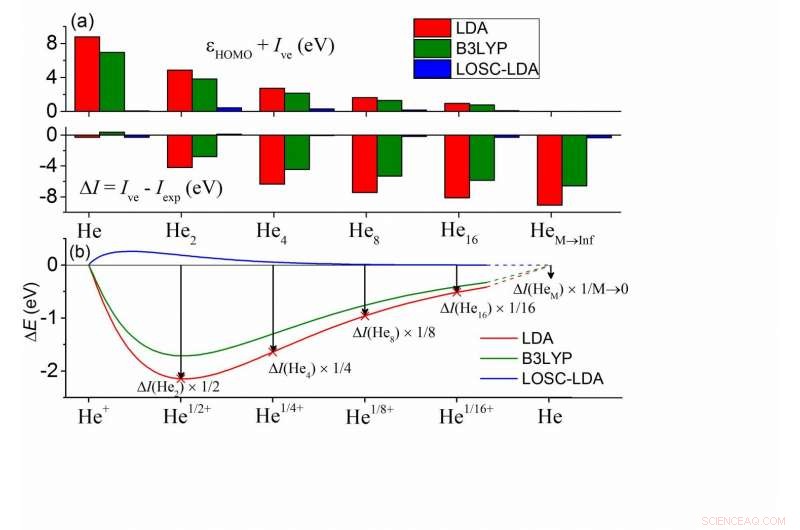
(a) Deviazioni tra ?HOMO e -Ive calcolati e tra Ive e Iexp per una serie di cluster HeM. In ogni cluster tutti gli atomi di He sono chimicamente equivalenti. Gli atomi vicini più vicini sono separati da 10Å, e l'Iexp di HeM è ben approssimato dall'Iexp di un atomo di He. (b) Deviazione di energia totale calcolata dalla condizione di linearità di un atomo di He con carica frazionata in funzione della carica frazionata δ. Qui ΔE(Heδ+) =E(Heδ+)-δE(He+)-(1-δ)E(He), ei valori sono stati scalati nella figura per un confronto diretto con (a). Credito:©Science China Press
La teoria del funzionale della densità di Kohn-Sham è una delle teorie di maggior successo in chimica. È formalmente rigoroso; il suo costo computazionale relativamente basso e l'accuratezza competitiva nei sistemi di piccole e medie dimensioni lo rendono uno dei metodi più popolari nei calcoli di strutture elettroniche, e forse l'unica scelta per modellare gli effetti quantistici degli elettroni in grandi sistemi chimici e biologici. Tuttavia, l'esatto funzionale non è noto in modo esplicito e le approssimazioni del funzionale di densità (DFA) allo stato dell'arte soffrono di errori sistematici. Uno degli errori dominanti nei DFA è l'errore di delocalizzazione, che è onnipresente e si manifesta in vari modi. Questo è stato un problema aperto impegnativo per decenni. Recentemente, Chen Li, Neil Qiang Su e Weitao Yang della Duke University e Xiao Zheng della University of Science and Technology of China hanno sviluppato un nuovo framework di correzione del ridimensionamento orbitale localizzato (LOSC) che dimostra l'eliminazione sistematica dell'errore di delocalizzazione.
Le principali conseguenze degli errori di delocalizzazione nei DFA possono essere classificate in due aspetti:(1) errore di energia orbitale di Kohn-Sham (KS) e (2) errore di energia totale. L'errore di delocalizzazione porta a importanti fallimenti nelle applicazioni pratiche come la sottovalutazione non fisica dei band gap, le distribuzioni di elettroni eccessivamente delocalizzate e gli errati trasferimenti di carica. Riguardo a questi due aspetti degli errori, entrambi si manifestano in modo dipendente dalle dimensioni. In particolare, tra le energie orbitali KS, la più alta energia dell'orbitale molecolare (HOMO) occupato, HOMO, dovrebbe concordare con il potenziale di ionizzazione verticale (negativo) (-Ive), come richiesto dall'esatto funzionale. Per di più, l'Ive calcolato dai DFA dovrebbe concordare con il valore sperimentale, Iexp.
Per i DFA di uso comune, le due condizioni non sono soddisfatte. Come mostrato dai calcoli del cluster di elio nella sottofigura (a), l'energia HOMO dall'approssimazione della densità locale (LDA) mostra un errore positivo rispetto a -Ive mentre Ive mostra un errore negativo, e i due errori vengono visualizzati in modo dipendente dalle dimensioni, suggerendo che l'errore di delocalizzazione dei DFA deve manifestarsi in un modo o nell'altro, o entrambi, mentre la somma delle grandezze rimane invariata. Inoltre, questo è prevalente in tutti i tipi di DFA, compreso il più popolare funzionale B3LYP, come mostrato in verde.
Per comprendere questi errori, i chimici possono mapparli negli errori di un atomo di He con carica frazionata, come illustrato nella sottofigura (b). Le energie del sistema frazionario dovrebbero scalare linearmente con il numero di elettroni frazionari n (0?n <1) per l'esatto funzionale. Nella sottofigura (b) è mostrata la deviazione di energia dalla condizione di linearità per un singolo atomo di He, dove le energie del sistema frazionario sono sottostimate- questo definisce l'errore di delocalizzazione. Inoltre, l'errore di carica frazionaria in (b) ha corrispondenza 1-1 con l'errore di energia totale ΔI =Ive - Iexp. Nel limite di M va all'infinito, si può dedurre che ΔI concorda con l'errore di pendenza della curva E(N) all'intero, che è esattamente l'errore di energia HOMO di un singolo atomo di He. Perciò, tutti gli errori sono interconnessi. È quindi possibile eliminare sistematicamente l'errore di delocalizzazione attraverso (1) la rimozione degli errori in (b) e (2) garantendo una rimozione coerente dell'errore in tutti i sistemi.
Nel presente lavoro di LOSC, gli autori hanno inventato nuove variabili locali, chiamati orbitali, che sono orbitali localizzati (LO) che raggiungono la località in spazi sia spaziali che energetici. Attraverso questi orbitali, sono stati in grado di esprimere la densità elettronica e la matrice di densità KS nella rappresentazione locale, dove sorge naturalmente la matrice di occupazione locale composta da numeri frazionari. Perciò, queste variabili locali sono in grado di catturare informazioni frazionarie locali in modo preciso e completo nello spazio orbitale, e fungono da elementi costitutivi perfetti per il funzionale LOSC. Per di più, riscrivendo i termini nei funzionali GSC e LSC in termini di formule di correzione della curvatura e facendo analogia al LOSC, hanno introdotto una matrice di curvatura locale, i cui elementi sono pensati come funzionali degli orbitalletti, essere in corrispondenza biunivoca con la matrice occupazionale locale. Finalmente, la formula LOSC è scritta come un'espressione esplicita ed elegante sul funzionale genitore in termini di queste due matrici.
Il LOSC raggiunge tutte le caratteristiche desiderabili. Nella figura sopra, gli errori LOSC-LDA sono essenzialmente trascurabili, indicando la validità e la consistenza della correzione. Questi sono stati anche convalidati dalle curve di dissociazione molto migliorate dei cationi molecolari biatomici, che vanno da H2+, He2+, catione dimero dell'acqua e catione dimero del benzene. L'HOMO, Gli errori energetici di LUMO sono stati molto ridotti e le buone prestazioni si mantengono man mano che le dimensioni del sistema crescono. Ciò è stato dimostrato da test su oligomeri di poliacene e trans-poliacetilene. Per di più, il LOSC è in grado di recuperare la giusta densità elettronica quando i DFA genitori lo rendono qualitativamente sbagliato, come mostrato dall'esempio di un anione cloro solvatato quando è privato di un elettrone.
Le prestazioni di LOSC mostrano quindi la promessa di eliminare sistematicamente l'errore di delocalizzazione all'interno dei funzionali di densità KS. Vale la pena notare che a differenza del paradigma tradizionale di progettazione di funzionali utilizzando la densità, i gradienti di densità, la densità di energia cinetica, eccetera., il framework LOSC coinvolge ingredienti completamente nuovi, gli orbitali, che a loro volta sono funzionali impliciti della matrice densità KS, e hanno dimostrato la loro capacità unica di affrontare problemi di vecchia data associati ai DFA tradizionali. Ciò riflette un cambiamento di paradigma nella progettazione di funzionali, e allarga enormemente la strada nell'esplorazione dell'esatto funzionale nel proprio spazio abitativo. In questo senso, LOSC ha inaugurato la tendenza nello sviluppo di una nuova generazione di approssimazioni funzionali di densità, promuovere la teoria del funzionale della densità a un nuovo livello di accuratezza.