
Una nuova tecnica per far crescere qualsiasi forma di destinazione da qualsiasi forma di partenza è dimostrata dal "far crescere" il volto del padre della fisica quantistica, Max Planck, da un disco piatto. Credito:Harvard SEAS
La natura ha un modo di creare forme complesse da un insieme di semplici regole di crescita. La curva di un petalo, la picchiata di un ramo, anche i contorni del nostro viso sono modellati da questi processi. E se potessimo sbloccare quelle regole e decodificare la capacità della natura di far crescere una gamma infinitamente diversa di forme?
Gli scienziati della Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) hanno fatto proprio questo. In un articolo pubblicato su Atti dell'Accademia Nazionale delle Scienze , un team di ricercatori del SEAS e del Wyss Institute for Biologically Inspired Engineering dimostra una tecnica per far crescere qualsiasi forma target da qualsiasi forma iniziale.
"L'architetto Louis Sullivan una volta disse che 'la forma segue sempre la funzione', " disse L. Mahadevan, la Lola England de Valpine Professore di Matematica Applicata, di Biologia Organismica ed Evoluzionistica e di Fisica e autore senior dello studio. "Ma se si prendesse la prospettiva opposta, che forse la funzione dovrebbe seguire la forma, come possiamo invertire la forma del disegno?"
In precedenti ricerche, il gruppo Mahadevan ha usato esperimenti e teoria per spiegare come le strutture si trasformano naturalmente, come le trappole per acchiappamosche di Venere, pigne e fiori, hanno cambiato forma nella speranza di essere un giorno in grado di controllare e imitare questi processi naturali. E senza dubbio, sperimentali hanno iniziato a sfruttare il potere di semplici, modelli di crescita bioispirati. Per esempio, nel 2016, in collaborazione con il gruppo di Jennifer Lewis, l'Hansjorg Wyss Professor of Biologically Inspired Engineering presso SEAS e Core Faculty Member del Wyss Institute, il team ha stampato una serie di strutture che hanno cambiato forma nel tempo in risposta agli stimoli ambientali.
"La sfida era come fare il problema inverso, " disse Wim van Rees, un borsista post-dottorato presso SEAS e primo autore del documento. "C'è molta ricerca sul lato sperimentale, ma non c'è abbastanza sul lato teorico per spiegare cosa sta realmente accadendo. La domanda è, se voglio finire con una forma specifica, come progetto la mia struttura iniziale?"
Ispirato dalla crescita delle foglie, i ricercatori hanno sviluppato una teoria su come modellare gli orientamenti di crescita e le grandezze di un doppio strato, due diversi strati di materiali elastici incollati tra loro che rispondono in modo diverso agli stessi stimoli. Programmando uno strato per gonfiarsi di più e/o in una direzione diversa rispetto all'altro, la forma e la curvatura complessive del doppio strato possono essere completamente controllate. In linea di principio, il doppio strato può essere di qualsiasi materiale, in qualsiasi forma, e rispondere a qualsiasi stimolo dal calore alla luce, rigonfiamento, o addirittura crescita biologica.
Il team ha svelato la connessione matematica tra il comportamento del doppio strato e quello di un singolo strato.
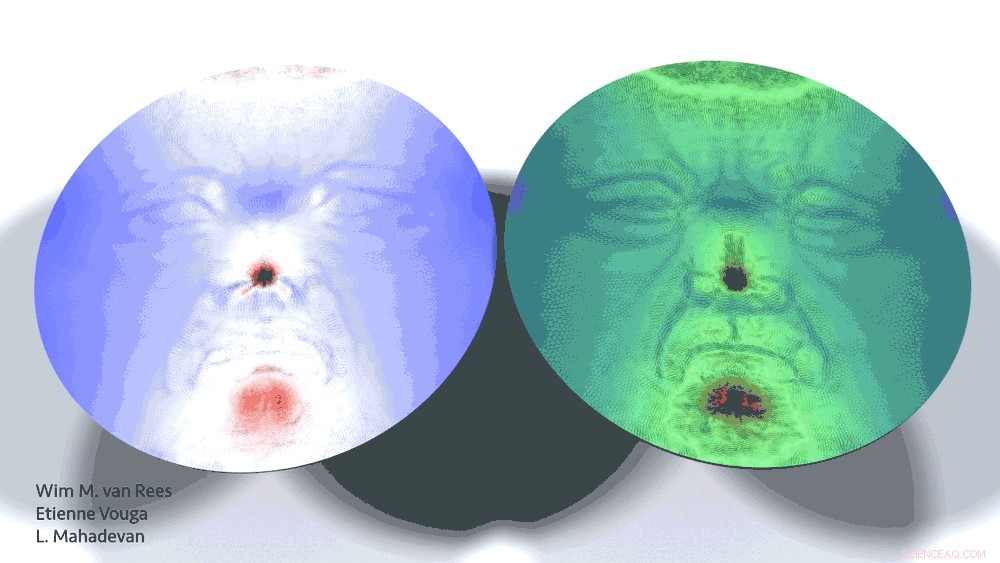
Il volto del padre della fisica quantistica, Max Planck, emerge da un disco piatto. In ogni stato, i colori mostrano i fattori di crescita dello strato superiore (sinistra) e inferiore (destra), e le sottili linee nere indicano la direzione della crescita. Lo strato superiore è visto dalla parte anteriore, e lo strato inferiore è visto da dietro, per evidenziare la complessità delle geometrie. Credito:Harvard SEAS
"Abbiamo trovato una relazione molto elegante in un materiale costituito da questi due strati, " ha detto van Rees. "Puoi prendere la crescita di un doppio strato e scrivere la sua energia direttamente nei termini di un monostrato curvo".
Ciò significa che se conosci le curvature di qualsiasi forma puoi decodificare l'energia e i modelli di crescita necessari per far crescere quella forma usando un doppio strato.
"Questo tipo di problema di reverse engineering è notoriamente difficile da risolvere, anche usando giorni di calcolo su un supercomputer, " disse Etienne Vouga, ex borsista postdottorato del gruppo, ora Assistant Professor di Informatica presso l'Università del Texas ad Austin. "Spiegando come la fisica e la geometria dei doppi strati sono intimamente accoppiate, siamo stati in grado di costruire un algoritmo che risolve il modello di crescita necessario in pochi secondi, anche su un laptop, non importa quanto sia complicata la forma del bersaglio."
I ricercatori hanno dimostrato il sistema modellando la crescita di un petalo di fiore di bocca di leone da un cilindro, una mappa topografica del bacino del fiume Colorado da un foglio piatto e, più sorprendentemente, il volto di Max Planck, uno dei fondatori della fisica quantistica, da un disco.
"Globale, la nostra ricerca combina la nostra conoscenza della geometria e della fisica dei gusci sottili con nuovi algoritmi e calcoli matematici per creare regole di progettazione per la forma ingegneristica, " ha affermato Mahadevan. "Apre la strada ai progressi nella produzione nella stampa 4-D di elementi ottici e meccanici che cambiano forma, robotica morbida e ingegneria dei tessuti".