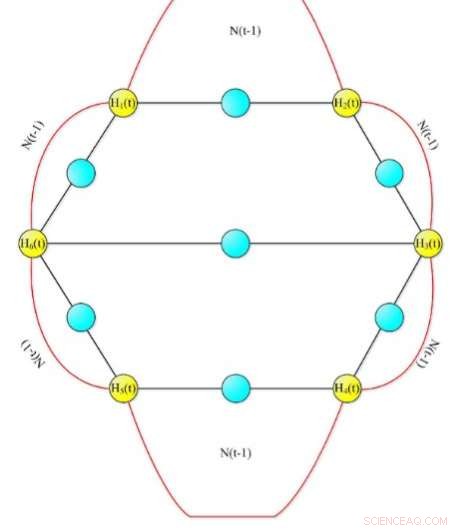
Diagramma del modello di rete casuale. Attestazione:Springer
Le reti sono spesso descritte come alberi con rami che si estendono. Il modo in cui l'albero si ramifica dipende dalla logica alla base dell'espansione della rete, come l'espansione casuale. Però, alcuni aspetti di tali reti in espansione casuale sono invarianti; in altre parole, presentano le stesse caratteristiche, indipendentemente dalle dimensioni della rete. Di conseguenza, l'intera rete ha la stessa forma di una o più delle sue parti.
In un nuovo studio pubblicato su EPJ SI , Fei Ma della Northwest Normal University di Lanzhou, provincia di Gansu, Cina, e colleghi calcolano il numero totale di spanning tree nelle reti in espansione casuale. Questo metodo può essere applicato alla modellazione di modelli di rete senza scala, quale, come risulta, sono caratterizzati da proprietà di piccolo mondo. Questo significa, ad esempio, che i membri della rete mostrano solo sei gradi di separazione, come la maggior parte delle persone nella nostra società.
In precedenza, un certo numero di modelli di rete erano basati su grafici costituiti da un'aggregazione di vertici con bordi di collegamento. Ma non erano sufficienti per modellare le reti della vita reale, come le reti di utenti dei social media. Anziché, reti complesse, dove la rete viene creata casualmente, sono diventati i pilastri dell'informatica e della moderna matematica discreta. Utilizzando i dati provenienti da reti reali, e attingendo all'esperienza acquisita da reti artificiali create per tenere conto di funzioni specifiche, gli autori progettano modelli più realistici che sono più complessi dei loro predecessori.
In questo studio, gli autori si concentrano sullo sviluppo di un metodo ricorsivo per calcolare il numero di spanning tree in una rete, che è particolarmente utile per prevedere la sua capacità di tollerare guasti che si verificano in modo casuale. Essere in grado di trovare il numero di spanning tree nei modelli di rete ha implicazioni per vari campi scientifici, come la matematica applicata, informatica teorica, fisica e chimica.