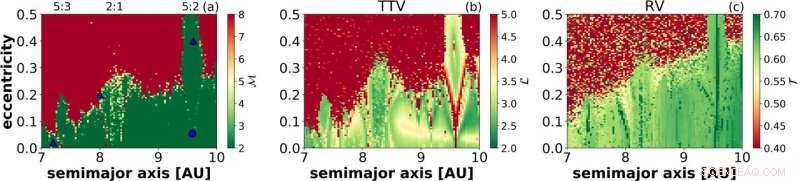
Una mappa di stabilità di Saturno ottenuta dall'indicatore di caos MEGNO (a) e dalla rete di ricorrenza misura la lunghezza media del percorso (b) e la transitività (c). Gli ultimi due pannelli si basano sulla variazione del tempo di transito di Giove e sulla velocità radiale del sole, rispettivamente. Attestazione:Tamás Kovács
Gli esopianeti che ruotano attorno a stelle lontane stanno venendo rapidamente messi a fuoco con tecnologie avanzate come il telescopio spaziale Kepler. Ottenere una piena comprensione di questi sistemi è difficile, perché le posizioni e le velocità iniziali degli esopianeti sono sconosciute. Determinare se le dinamiche del sistema sono quasi periodiche o caotiche è complicato, costoso e computazionalmente impegnativo.
In questa settimana Caos , Tamás Kovács offre un metodo alternativo per l'analisi della stabilità dei corpi esoplanetari utilizzando solo i dati delle serie temporali osservate per dedurre misurazioni dinamiche e quantificare l'imprevedibilità dei sistemi di esopianeti.
"Se non conosciamo le equazioni che governano il moto di un sistema, e abbiamo solo le serie temporali, ciò che misuriamo con il telescopio, quindi vogliamo trasformare quelle serie temporali in una rete complessa. In questo caso, si chiama rete di ricorrenza, " ha detto Kovács. "Questa rete contiene tutte le caratteristiche dinamiche del sistema sottostante che vogliamo analizzare".
Il documento si basa sul lavoro del fisico Floris Takens, che propose nel 1981 di ricostruire la dinamica di un sistema utilizzando una serie di osservazioni sullo stato del sistema. Con il teorema di immersione di Takens come punto di partenza, Kovács utilizza l'incorporamento del ritardo temporale per ricostruire una traiettoria ad alta dimensione e quindi identificare i punti di ricorrenza, dove i corpi nello spazio delle fasi sono vicini l'uno all'altro.
"Quei punti speciali saranno i vertici e i bordi della rete complessa, " ha detto Kovács. "Una volta che hai la rete, puoi riprogrammare questa rete per poter applicare misure come la transitività, lunghezza media del percorso o altri univoci per quella rete."
Kovács verifica l'affidabilità del metodo utilizzando un sistema noto come modello, il sistema dei tre corpi di Saturno, Giove e il sole, e poi lo applica al sistema Kepler 36b e 36c. I risultati del suo sistema Keplero concordano con quanto noto.
"Studi precedenti hanno evidenziato che Kepler 36b e 36c è un sistema molto speciale, perché dalla simulazione diretta e dalle integrazioni numeriche, vediamo che il sistema è ai margini del caos, " ha detto Kovács. "A volte, mostra una dinamica regolare, e altre volte, sembra essere caotico."
L'autore prevede di applicare successivamente i suoi metodi a sistemi con più di tre corpi, testare la sua scalabilità ed esplorare la sua capacità di gestire serie temporali più lunghe e set di dati più nitidi.