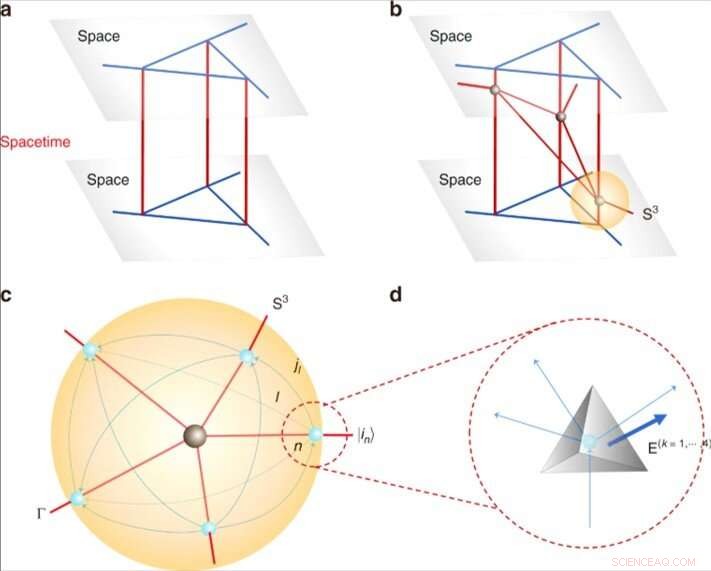
Spaziotempo quantistico e tetraedri. (a) Uno spaziotempo quantistico statico 4d dall'evoluzione della rete di spin. (b) Uno spaziotempo quantistico dinamico con un numero di cinque vertici valenti (in nero) intersecando fogli del mondo, uno dei quali è indicato con S3. (c) La struttura locale di un vertice da b considerando una 3-sfera S3 che racchiude il vertice. Le intersezioni tra i fogli del mondo e S3 danno una rete di spin (in blu). Ogni rete di spin rappresenta uno stato |in⟩ e ogni collegamento l è orientato, che porta un semiintero jl. (d) Tetraedri geometrici quantistici. Ogni nodo della rete di spin rappresenta un tetraedro quantistico. Collegare 2 nodi tramite un collegamento nella rete di spin corrisponde ad incollare 2 tetraedri attraverso la faccia duale al collegamento. Le aree orientate sono indicate con E(k=1, , 4)=(E(k)x, E(k)y, E(k)z). Credito:Fisica della Comunicazione, doi:10.1038/s42005-019-0218-5
La simulazione quantistica svolge un ruolo insostituibile in diversi campi, oltre l'ambito dei computer classici. In un recente studio, Keren Li e un team di ricerca interdisciplinare presso il Center for Quantum Computing, Scienza e ingegneria quantistica e il Dipartimento di Fisica e Astronomia in Cina, Stati Uniti Germania e Canada. Stati della rete di spin simulati sperimentalmente mediante la simulazione di tetraedri spazio-temporali quantistici su un simulatore quantistico di risonanza magnetica nucleare (NMR) a quattro qubit. La fedeltà sperimentale era superiore al 95 percento. Il team di ricerca ha utilizzato il tetraedro quantistico preparato dalla risonanza magnetica nucleare per simulare un'ampiezza (modello) del vertice della schiuma di spin bidimensionale (2D), e visualizzare le dinamiche locali dello spaziotempo quantistico. Li et al. misurato le proprietà geometriche dei corrispondenti tetraedri quantistici per simulare le loro interazioni. Il lavoro sperimentale è un tentativo iniziale e un modulo base per rappresentare il vertice del diagramma di Feynman nella formulazione spinfoam, studiare la gravità quantistica del ciclo (LQG) utilizzando l'elaborazione delle informazioni quantistiche. I risultati sono ora disponibili su Fisica della Comunicazione.
I computer classici non possono studiare grandi sistemi quantistici nonostante le simulazioni riuscite di una varietà di sistemi fisici. I vincoli sistematici dei computer classici si sono verificati quando la crescita lineare delle dimensioni del sistema quantistico corrispondeva alla crescita esponenziale dello spazio di Hilbert, un fondamento matematico della meccanica quantistica. I fisici quantistici mirano a superare il problema utilizzando computer quantistici che elaborano le informazioni in modo intrinsecamente o meccanicamente quantistico per superare in modo esponenziale le loro controparti classiche. Nel 1982, Il fisico Richard Feynman ha definito i computer quantistici come sistemi quantistici che possono essere controllati per imitare o simulare il comportamento o le proprietà di sistemi quantistici relativamente meno accessibili.
Nel presente lavoro, Li et al. ha utilizzato la risonanza magnetica nucleare (NMR) con un'elevata prestazione controllabile sul sistema quantistico per sviluppare metodi di simulazione. La strategia ha facilitato la presentazione di geometrie quantistiche dello spazio e dello spaziotempo basate sulle analogie tra gli stati di spin nucleare nei campioni NMR e gli stati della rete di spin nella gravità quantistica. La gravità quantistica mira a unire la gravità di Einstein con la meccanica quantistica per espandere la nostra comprensione della gravità alla scala di Planck (1,22 x 10 19 GeV). Alla scala di Planck (grandezze dello spazio, tempo ed energia) La gravità di Einstein e il continuum della rottura dello spaziotempo possono essere sostituiti tramite lo spaziotempo quantistico. Gli approcci di ricerca per la comprensione degli spazi-tempi quantistici sono attualmente radicati nelle reti di spin (un grafico di linee e nodi per rappresentare lo stato quantistico dello spazio in un determinato momento), che sono un importante, quadro non perturbativo della gravità quantistica.
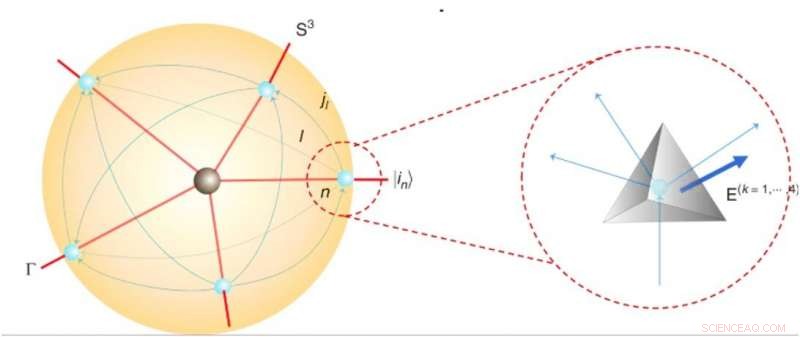
Spaziotempo quantistico e tetraedri all'interno di una rete di spin. Credito:Fisica della Comunicazione, doi:10.1038/s42005-019-0218-5
Nel 1971, il fisico Roger Penrose ha proposto reti di spin motivate dalla teoria del twistor con successive applicazioni al loop della gravità quantistica (LQG). Le reti di spin erano stati quantistici che rappresentavano geometrie quantistiche fondamentalmente discrete dello spazio alla scala di Planck. In questo studio, il team di ricerca ha rappresentato la rete di spin utilizzando un grafico con collegamenti e nodi colorati dalle metà di spin. Per esempio, qualsiasi nodo con bordi corrispondeva a una geometria e quindi un grafo contenente nodi quadrivalenti corrispondeva alla geometria del tetraedro quantistico.
Il team di ricerca ha sviluppato una "rete" contenente una serie di fogli del mondo tridimensionali (3-D) (superfici 2-D) e le loro intersezioni. Hanno mostrato che ogni vertice in cui le superfici si incontravano, ha portato a una transizione quantistica che ha cambiato la rete di spin per rappresentare le dinamiche locali della geometria quantistica. Proprio come i diagrammi di Feynman (rappresentazioni schematiche di espressioni matematiche che descrivono il comportamento delle particelle subatomiche), lo spaziotempo quantistico ha codificato le ampiezze di transizione e le ampiezze di spinfoam tra le reti di spin iniziale e finale. Gli spazitempo quantistici e le ampiezze della schiuma spin sviluppate nello studio hanno fornito un approccio coerente e promettente alla gravità quantistica. Li et al. caratterizzato la simulazione NMR dalla capacità di controllare singoli qubit con alta precisione. I tetraedri quantistici e le ampiezze dei vertici sono serviti come elementi costitutivi di LQG (gravità quantistica ad anello) per aprire una nuova finestra per includere LQG negli esperimenti quantistici.
Gli scienziati hanno prima derivato equazioni per descrivere un tetraedro quantistico all'interno di una rete di spin. In un modello schematico di spaziotempo quantistico dinamico 3+1 dimensionale, hanno dimostrato un atomo come una 3-sfera che racchiude una porzione dello spaziotempo quantistico che circonda un vertice. Il team ha modellato il confine dello spaziotempo quantistico racchiuso proprio come una rete di spin e ha mostrato la possibilità di simulare grandi spazitempo quantistici con molti vertici incollando quantisticamente gli atomi. La struttura risultante assomigliava all'ampiezza del vertice dello spaziotempo quantistico simile ai modelli reticolari topologici di Ooguri precedentemente sviluppati in quattro dimensioni. I ricercatori hanno mostrato a LQG di identificare le geometrie del tetraedro quantistico con i momenti angolari quantistici. L'identificazione ha permesso loro di simulare geometrie quantistiche con registri quantistici (analogo meccanico quantistico di un registro di processore classico). Generalmente, un registro quantistico può essere ottenuto matematicamente utilizzando prodotti tensoriali.
IN ALTO:Stati preparati sperimentalmente sulla sfera di Bloch e sui corrispondenti tetraedri classici. Gli stati assumono la forma cosθ2|0⟩L+eiϕsinθ2|1⟩L e sono indicati da Ai, Bi, Ci, Di, Ei (i=0, 1), tra i quali, C0 e C1 sono tetraedri regolari. |0L⟩ e |1L⟩ sono gli stati base in un sottospazio di un sistema a quattro qubit, che rappresenta un singolo qubit logico. BOTTOM:Valori del coseno degli angoli tra le normali delle facce nel tetraedro quantistico (i coseni degli angoli diedri differiscono per un segno meno). I risultati degli esperimenti (teoria) sono rappresentati dalle colonne colorate (trasparenti). Le barre di errore derivano dall'incertezza durante l'adattamento degli spettri di risonanza magnetica nucleare (NMR). Credito:Fisica della Comunicazione, doi:10.1038/s42005-019-0218-5 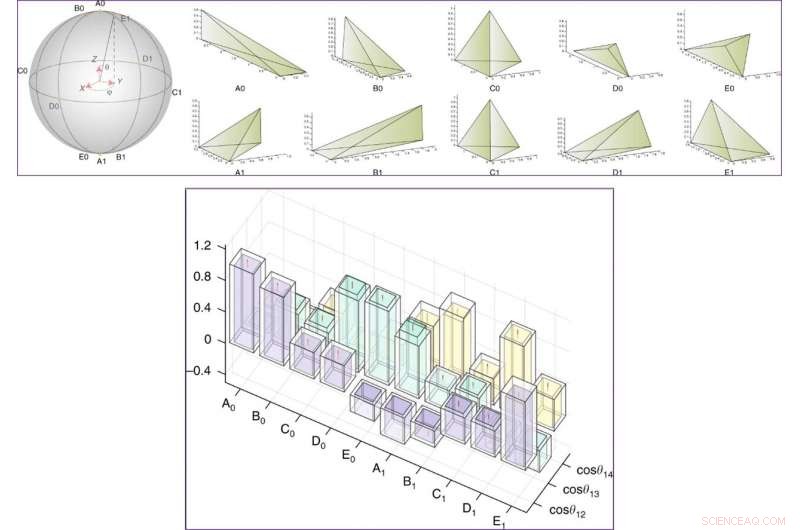
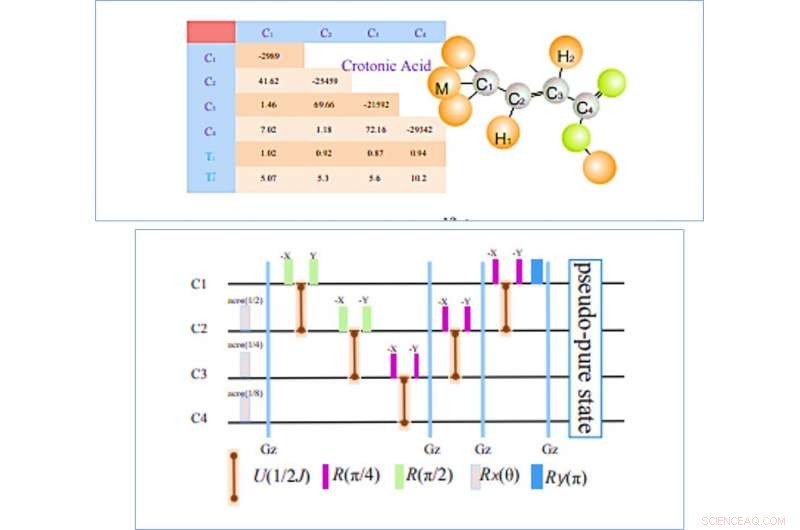
A SINISTRA:Struttura della molecola dell'Acido Crotonico; I quattro nuclei 13C sono indicati come i quattro qubit e la tabella a sinistra presenta i parametri che costruiscono l'Hamiltoniana interna. Spostamenti chimici (Hz), Le forze di accoppiamento J (Hz) e i tempi di rilassamento (T1 e T2) sono elencati nella parte diagonale, elementi fuori diagonale e il fondo, rispettivamente. Tutti i parametri sono stati misurati su uno spettrometro Bruker DRX 700 MHz a temperatura ambiente. A DESTRA:sequenze di impulsi per la creazione dello stato pseudo-puro. Sulla base della tecnica della media spaziale, i circuiti includono operazioni locali, cinque evoluzioni del giunto a J, e quattro impulsi in gradiente z per distruggere i termini coerenti indesiderati. la durata dell'evoluzione libera di 1/2J dipende dalla forza dell'accoppiamento a J tra i relativi giri. Credito:Fisica della Comunicazione, doi:10.1038/s42005-019-0218-5
Per ottenere le ampiezze dei vertici, i ricercatori hanno calcolato i prodotti interni tra cinque diversi stati del tetraedro quantistico. Idealmente, i ricercatori avrebbero potuto usare un computer quantistico da 20 qubit, stabilire stati di massima entanglement di due qubit tra due tetraedri arbitrari. Però, poiché un computer quantistico di tali dimensioni è attualmente al di là della tecnologia d'avanguardia commercializzata, i ricercatori hanno condotto alternativamente la tomografia completa della preparazione dello stato per ottenere informazioni sugli stati del tetraedro quantistico. Quando gli scienziati hanno calcolato le fedeltà tra gli stati sperimentali del tetraedro quantistico e la teoria, i risultati sono stati ben al di sopra del 95 per cento. Usando i tetraedri quantistici, il team di ricerca ha simulato l'ampiezza del vertice. Hanno confrontato i risultati tra l'esperimento e la simulazione numerica tra tutti e cinque i tetraedri. Di conseguenza, punti di sella dell'ampiezza negli esperimenti si sono verificati in cui i cinque tetraedri interagenti hanno dimostrato un semplice significato geometrico mentre si incollavano per formare un geometrico quadri-simplex.
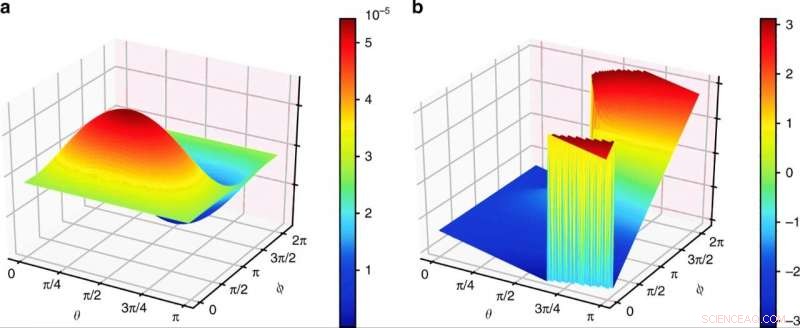
I risultati delle ampiezze dei vertici simulate a sono l'ampiezza dell'eq. (3) eb descrivono le informazioni della sua fase. e ϕ sono i parametri dello stato tensore invariante a quattro qubit corrispondenti alle coordinate sferiche sulla sfera di Bloch. Credito:Fisica della Comunicazione, doi:10.1038/s42005-019-0218-5
In questo modo, Keren Li e collaboratori hanno utilizzato un registro quantistico nel sistema NMR per creare 10 stati tensoriali invarianti per rappresentare 10 tetraedri quantistici. Hanno raggiunto una fedeltà superiore al 95% e successivamente hanno misurato gli angoli diedri (due facce piane) del modello. Hanno considerato gli errori di adattamento dello spettro e l'identificazione geometrica per comprendere il successo nella simulazione dei tetraedri quantistici nello studio. Il nuovo lavoro di ricerca ha presentato un primo passo per esplorare gli stati della rete di spin e le ampiezze della schiuma di spin utilizzando un simulatore quantistico. Il lavoro di accompagnamento ha anche dimostrato validi esperimenti per studiare LGQ.
© 2019 Scienza X Rete