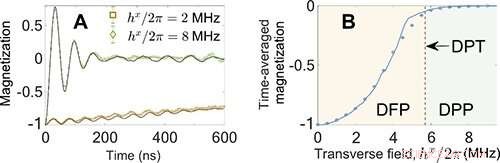
Fig. 1 Evoluzione temporale della magnetizzazione e magnetizzazione media nel tempo in funzione del campo trasversale. Credito:IOP
La simulazione quantistica utilizza un sistema quantistico controllabile per imitare sistemi complessi o risolvere problemi intrattabili, tra i quali i problemi di non equilibrio dei sistemi quantistici a molti corpi hanno attratto ampio interesse di ricerca. Tali sistemi sono difficili da simulare utilizzando computer classici. Anziché, simulatori quantistici popolari, come circuiti superconduttori, può fornire approfondimenti su questi problemi. Poiché sono stati compiuti notevoli progressi nella scalabilità, coerenza e controllabilità, i circuiti superconduttori sono diventati una delle più importanti piattaforme di simulazione quantistica.
Recentemente, un gruppo di ricerca dell'Istituto di Fisica dell'Accademia Cinese delle Scienze, Zhejiang University e RIKEN in Giappone, ha eseguito con successo la simulazione quantistica delle transizioni di fase dinamiche in un modello Lipkin-Meshkov-Glick con un simulatore quantistico superconduttore a 16 qubit.
La transizione di fase dinamica (DPT) è un tipo di transizione di fase di non equilibrio ed è stata teoricamente studiata in vari modelli quantistici a molti corpi. Esistono due tipi di DPT. Il primo tipo (DPT-1) si concentra sul parametro dell'ordine di non equilibrio, mentre il secondo tipo (DPT-2) è caratterizzato dai comportamenti non analitici dell'eco di Loschmidt associato agli zeri di Lee-Yang-Fisher in meccanica statistica. Ulteriori indagini teoriche e numeriche hanno rivelato che DPT-1 e DPT-2 possono essere studiati nello stesso framework.
Il processore quantistico integra 20 qubit superconduttori tutti accoppiati a un comune bus risonatore, che è stato utilizzato per generare stati di gatto Schrödinger in lavori precedenti. Questa volta, Sono stati utilizzati 16 qubit per progettare il modello Lipkin-Meshkov-Glick (LMG) applicando un campo trasversale controllabile a ciascun qubit. Il sistema è portato in uno stato di non equilibrio con le microonde e poi si è evoluto secondo il modello LMG.
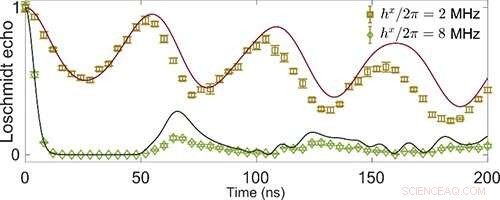
Fig. 2 Evoluzione temporale dell'eco di Loschmidt. Credito:IOP
I ricercatori hanno prima osservato le caratteristiche tipiche del DPT-1. Per il piccolo campo trasversale, il sistema rimane nella fase ferromagnetica dinamica (DFP), e la magnetizzazione mostra un lento rilassamento. Però, dato un forte campo trasversale, il sistema entra nella fase paramagnetica dinamica (DPP), in cui la magnetizzazione mostra una grande oscillazione in un primo momento e si avvicina a zero nel limite di lungo periodo. La magnetizzazione media nel tempo come parametro d'ordine di non equilibrio è zero nel DPP, mentre diventa finito in DFP.
Poi hanno dimostrato l'esistenza degli zeri dell'eco di Loschmidt nel DPP, suggerendo la relazione tra DPT-1 e DPT-2. Inoltre, i ricercatori hanno esplorato i DPT da una nuova prospettiva. Hanno studiato lo spin squeezing minimo come sonda della transizione di fase.
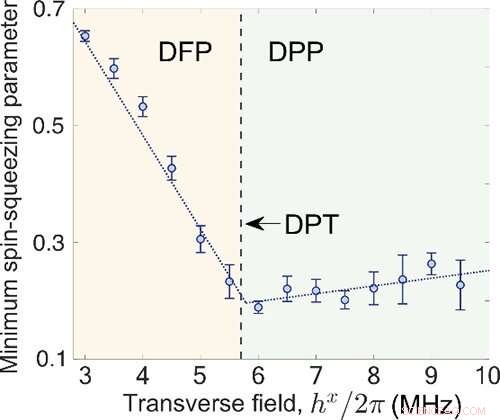
Fig. 3 Il parametro di spin-squeezing minimo in funzione del campo trasversale. Credito:IOP
I risultati sperimentali mostrano che il valore minimo dei parametri di spin-squeezing può essere raggiunto molto vicino al punto critico del DPT. Ciò indica una potenziale applicazione del DPT alla metrologia quantistica.
Questo studio, intitolato "Sondaggio di transizioni di fase dinamiche con un simulatore quantistico superconduttore, " è stato pubblicato in Progressi scientifici .