
Credito:CC0 Dominio Pubblico
I superconduttori topologici (TSC) sono un nuovo tipo di stati quantistici topologici con struttura a bande gapped completamente superconduttiva nella massa, ma supportano eccitazioni gapless chiamate modalità zero Majorana (MZM) ai confini. A causa della loro correlazione non locale e della natura statistica non abeliana, Gli MZM sono proposti come qubit della computazione quantistica topologica. Quindi, la ricerca e il funzionamento degli MZM nei materiali TSC è ora un argomento importante nella fisica della materia condensata.
Per identificare un TSC, bisognerebbe prima accertarne la classificazione topologica. La classificazione topologica dipende fortemente dalle simmetrie inclusa la simmetria di inversione temporale, simmetria particella-foro, e soprattutto le simmetrie cristalline. Senza considerare le simmetrie cristalline, le Hamiltoniane di Bogoliubov-deGennes (BdG) dei superconduttori 1-D hanno solo la classificazione Z2. La simmetria di riflessione dello specchio e le simmetrie rotazionali possono migliorare la classificazione in classe Z. Tuttavia, la classificazione topologica dei superconduttori con simmetrie magnetiche generali è ancora una questione aperta.
In un nuovo articolo di ricerca pubblicato nella rivista con sede a Pechino Rassegna scientifica nazionale , scienziati della Huazhong University of Science and Technology di Wuhan, Cina, e la Princeton University nel New Jersey, Gli USA hanno proposto il metodo per classificare la fase topologica superconduttiva esaminando la compatibilità tra diversi MZM. Co-autori Jinyu Zou, Qing Xie, Zhida Song e Gang Xu hanno analizzato la classificazione topologica dei fili superconduttori gapped con simmetrie magnetiche locali (LMS). Hanno scoperto che un'efficace classe BDI TSC può essere realizzata in M X T o C 2z T invariante filo. Sorprendentemente, le nuove fasi TSC caratterizzate da Zh invariante in C 4z Vengono scoperti il caso T e l'invariante Zhoplus Zc nel caso C6zT.
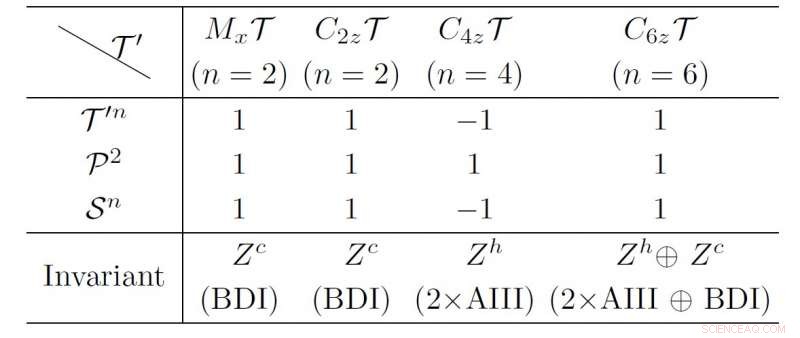
La classificazione topologica dei sistemi superconduttori gapped 1D con gli LMS. Credito:©Science China Press
Nell'articolo intitolato "Nuovi tipi di superconduttori topologici sotto simmetrie magnetiche locali". Gli autori si concentrano sui fili superconduttori 1D con LMS T'=M X T, C 2z T, C 4z T e C 6z T. "L'operazione di T' non cambia la posizione degli elettroni. Quindi agisce sull'Hamiltoniana BdG come un operatore di inversione temporale". Combinando T' e la simmetria particella-buca P si ottiene una simmetria chirale S =T'P. L'Hamiltoniana BdG può adottare la forma diagonalizzata secondo la simmetria chirale. E gli MZM sono gli autostati della simmetria chirale S. Gli autori trovano che "gli MZM con autovalori chirali s e -s possono accoppiarsi tra loro ed essere eliminati". Seguendo la linea guida, analizzano la compatibilità degli MZM alla fine dei fili superconduttori 1D con gli LMS, e riassumere la loro classificazione topologica come elencato nella tabella I.
Loro X T e C 2z I casi T sono equivalenti alla classe BDI con invariante topologico chirale Zc. Mentre il case C4zT è caratterizzato da Z . elicoidale h invariante, che indicano più coppie Majorana Kramer all'estremità del filo superconduttore. nel C 6z caso T, "la topologia dell'intera Hamiltoniana BdG è classificata da Z h oplus Z C , ". In una tale nuova fase topologica, "gli MZM elicoidali e chirali possono coesistere".
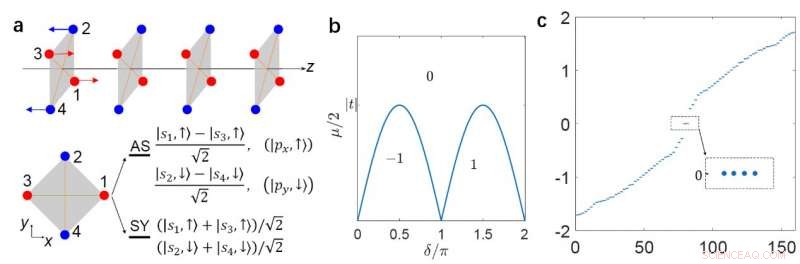
(a) Un filo superconduttore che preserva C4zT allineato lungo la direzione z. (b) Il diagramma di fase topologico. (c) lo spettro della fase non banale con un confine aperto su entrambi i lati, in cui compaiono quattro MZM a energia zero. Credito:©Science China Press
"Illustrare la fase TSC con l'LMS C 4z T, costruiamo una catena antiferromagnetica 1D lungo la direzione z, " aggiungono gli scienziati. Forniscono il diagramma di fase topologico del modello. "Nella fase TSC non banale, il filo quantistico aperto intrappola una coppia intera di MZM alle sue estremità." mostrano anche gli MZM attraverso calcoli numerici e analitici.
"Questi risultati non solo arricchiscono la varietà del TSC 1-D, ma forniscono anche lussureggianti elementi costitutivi per la costruzione di nuovi TSC di tipo 2-D e 3-D" prevedono alla fine dell'articolo, "Per esempio, si possono accoppiare i TSC 1D in direzione y per costruire un TSC 2-D. Le linee ad alta simmetria ky =0 e ky =pi nello spazio del momento preservano l'LMS 1D. Con parametri adeguati, le linee ky =0 e ky =pi possono appartenere a fasi topologiche distinte, e si traducono negli stati edge di Majorana che si propagano senza pause che collegano le bande conduttrici e le bande di valenza."