Vengono esaminate le strutture teoriche delle proprietà chiroottiche dei materiali e dei campi elettromagnetici. Sulla base di questi fondamenti, i sistemi chirottici possono essere compresi, e complicati fenomeni chirottici possono essere descritti.

I recenti progressi nei nanomateriali artificiali e nei campi ottici strutturati hanno ampliato il concetto di fenomeni chirottici. Però, i fenomeni chirottici originano da complicati processi che comportano transizioni tra stati con parità opposte, quindi sono necessari i fondamenti dei processi chirottici per una solida interpretazione dei fenomeni. Qui, i quadri teorici sulle proprietà chiroottiche dei materiali elettromagnetici sono discussi nel contesto dei sistemi microscopici (disperdenti chirottici discreti) e macroscopici (mezzi chirottici continui).

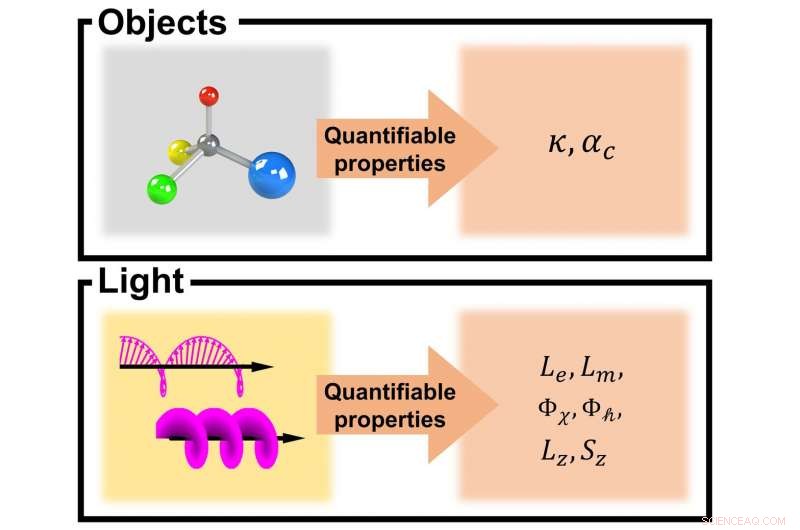
Un "oggetto chirale" si riferisce a un oggetto tridimensionale che non può essere sovrapposto alla sua immagine speculare utilizzando solo traslazioni e rotazioni. Tali oggetti chirali interagiscono in modo diverso con le luci polarizzate circolarmente sinistra e destra, e la differenza di assorbimento a queste due polarizzazioni circolari (dicroismo circolare) è stata ampiamente utilizzata per caratterizzare le proprietà chirottiche degli oggetti chirali. Però, la chiralità (geometrica) è una proprietà qualitativa; questo è, non diciamo che la propria mano è più chirale della mano di un altro. D'altra parte, gli effetti chirottici osservati sono quantità misurabili. Introducendo parametri chirottici, gli effetti chirottici possono essere descritti e il grado di chiralità elettromagnetica può essere definito e quantificato.

Inoltre, le proprietà chiroottiche dei campi elettromagnetici sono discusse nel contesto della densità locale della chiralità di campo e del suo flusso, che sono state definite come la chiralità ottica e l'elicità ottica. Anche, fasci elicoidali con momento angolare orbitale intrinseco sono discussi come un'altra classe di luce chirale.

Parlando in generale, un fenomeno chirale coinvolge due oggetti chirali, dove un oggetto chirale interagisce in modo diverso con un altro oggetto chirale e il suo enantiomero (immagine speculare). Nei fenomeni chirottici, uno degli oggetti chirali è la luce stessa. Riconoscendo che la luce può anche essere chirale, si può anche quantificare il grado di chiralità del campo.

Diversi fenomeni chirottici sono discussi nell'ambito dell'utilizzo degli identici parametri chirottici dei campi e dei materiali. Questo approccio fornisce una chiara comprensione di diversi fenomeni chirottici tra cui la chiralità intrinseca ed estrinseca, diffusione enantioselettiva, rilevamento molecolare, ed effetti optomeccanici. Questo articolo di revisione sarà utile per comprendere fenomeni chirottici complicati e per progettare e ottimizzare sistemi e campi chirottici con figure di merito ben definite.