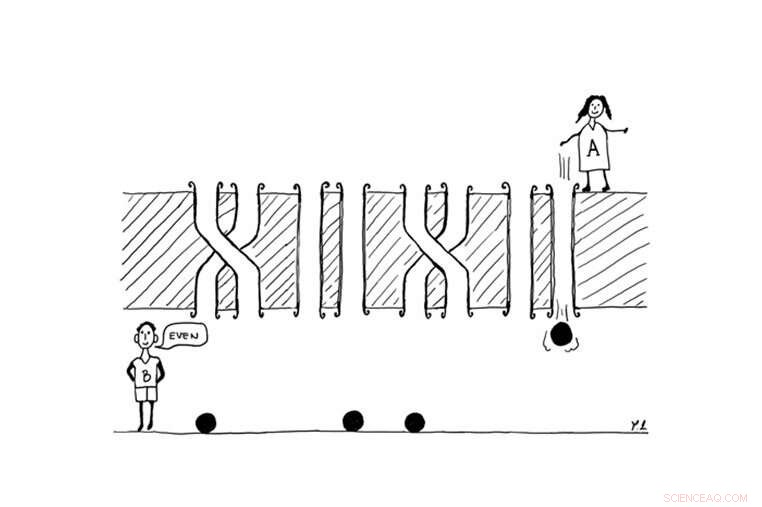
La figura rappresenta l'esempio più semplice di giochi di parità. Alice (A) lancia un certo numero di biglie verso Bob (B), con l'obiettivo di sapere se il numero di tubi ritorti è pari o dispari. I giocatori hanno bisogno di quattro biglie classiche ordinarie per completare il compito. In contrasto, già due biglie quantistiche sarebbero sufficienti. Credito:© Borivoje Dakić
Come ha affermato Richard Feynman, "l'esperimento della doppia fenditura è assolutamente impossibile da spiegare in alcun modo classico e ha in sé il cuore della meccanica quantistica. In realtà, contiene l'unico mistero."
Infatti, in questo esperimento, una particella quantistica si comporta come se si trovasse contemporaneamente in due luoghi distinti, e mostra fenomeni paradigmatici simili a onde come l'interferenza. Però, è stato poi notato che gli esperimenti multi-fessura mostrano che il grado di delocalizzazione delle particelle quantistiche ha i suoi limiti, e che in un certo senso, le particelle quantistiche non possono essere delocalizzate contemporaneamente in più di due posizioni. Questa limitazione ha creato un enigma che fino ad oggi non è stato ancora completamente risolto. I ricercatori dell'Università di Vienna e dell'IQOQI-Vienna (Accademia austriaca delle scienze) hanno compiuto un passo significativo verso la comprensione di questo problema riformulando gli esperimenti di interferenza in termini di giochi di teoria dell'informazione. La loro analisi, che è recentemente apparso sulla rivista Quantum, fornisce un modo intuitivo di pensare ai fenomeni di interferenza e ai suoi limiti, aprendo così la strada alla soluzione del suddetto enigma.
Una delle caratteristiche più sorprendenti della meccanica quantistica è il principio di sovrapposizione. Questo principio può essere illustrato più facilmente tramite l'esperimento della doppia fenditura, che coinvolge una particella che viene inviata attraverso una piastra forata con due fenditure. Secondo le nostre comuni intuizioni quotidiane, ci si potrebbe aspettare che la particella passi sempre o attraverso una fenditura, o attraverso l'altro. Però, la meccanica quantistica implica che la particella possa in un certo senso passare attraverso entrambe le fenditure contemporaneamente, questo è, può essere in una sovrapposizione di due posizioni contemporaneamente. Questa possibilità è alla base del fenomeno dell'interferenza quantistica, cioè il sorprendente comportamento ondulatorio esibito dalle particelle quantistiche. Ora, c'è un modo per quantificare il grado in cui le particelle quantistiche possono essere delocalizzate? La teoria quantistica consente alle particelle di attraversare più di due percorsi contemporaneamente? Per comprendere queste domande, i fisici hanno analizzato "esperimenti multi-fessura, ", che differiscono dall'esperimento della doppia fenditura solo per il numero di fenditure:ad esempio, un esperimento a tripla fenditura coinvolge una particella inviata attraverso tre fenditure.
Si potrebbe pensare che se una particella quantistica può passare attraverso due fenditure contemporaneamente, dovrebbe anche essere in grado di passare simultaneamente attraverso tre, quattro, o un numero qualsiasi di fessure. Sorprendentemente, è stato subito notato che qualsiasi pattern ottenuto in esperimenti multi-fessura può essere spiegato dal fatto che la particella passa sempre attraverso al massimo due fenditure contemporaneamente. Anche se questa caratteristica è matematicamente completamente compresa, le seguenti domande rimangono senza risposta:c'è una ragione fisica per l'apparente asimmetria tra l'esperimento della doppia fenditura e gli esperimenti con più fenditure? Cosa sta alla base di questa limitazione alquanto arbitraria sulla "delocalizzazione" delle particelle quantistiche?
Nel loro recente lavoro, Sebastian Horvat e Borivoje Dakić, ricercatori dell'Università di Vienna e dell'IQOQI-Vienna (Accademia austriaca delle scienze), hanno compiuto un passo significativo verso la comprensione di questo problema affrontandolo con la teoria dell'informazione. Vale a dire, hanno riformulato fenomeni di interferenza ed esperimenti multi-fessura in termini di "giochi di parità", la cui istanza più semplice è illustrata in figura. Il gioco coinvolge due giocatori, Alice e Bob, che sono separati da un muro forato da quattro paia di tubi. Ogni coppia di tubi può essere dritta o attorcigliata, e il numero di doppini è sconosciuto sia ad Alice che a Bob. Per di più, Alice ha a disposizione un certo numero di biglie che può far scorrere attraverso i tubi verso Bob; i giocatori possono usare queste biglie per imparare qualcosa sulla struttura dei tubi.
L'obiettivo del gioco è che i giocatori collaborino e scoprano se il numero totale di doppini è pari o dispari, utilizzando il minor numero possibile di biglie. Ora, supponiamo che Alice lanci una biglia attraverso uno dei tubi, per esempio attraverso il secondo. Bob può quindi dedurre facilmente se la prima coppia di tubi è dritta o attorcigliata semplicemente controllando se la biglia è caduta attraverso il secondo tubo o attraverso il primo. Analogamente, se Alice ha a disposizione quattro biglie, può far scorrere ciascuno di loro attraverso il tubo destro di ogni coppia (come nel caso della figura). Bob può quindi dedurre direttamente il numero di doppini intrecciati, e quindi se questo numero è pari o dispari, vincendo così la partita. Però, se il numero di coppie di tubi supera il numero di biglie che Alice ha a disposizione, allora il gioco non può essere vinto, poiché ci sarà sempre almeno una coppia di tubi, su cui Bob non può raccogliere alcuna informazione. Perciò, per vincere la partita, i giocatori devono usare tante biglie quante sono le coppie di tubi.
D'altra parte, meccanica quantistica, e più specificamente, il principio di sovrapposizione, permette ai giocatori di vincere la partita illustrata in figura utilizzando solo due "marmi quantistiche"! Un modo per capire da dove proviene questo miglioramento è ricordare, come si diceva prima, che una particella quantistica può "passare attraverso due luoghi contemporaneamente". Due biglie quantiche possono quindi "passare simultaneamente attraverso quattro posizioni", imitando così il comportamento di quattro marmi ordinari (classici). "In questo gioco, le biglie si comportano in modo analogo ai gettoni che possono essere inseriti attraverso i tubi. Quando Alice inserisce un normale marmo classico, è come se avesse inserito 1 centesimo.
D'altra parte, poiché la teoria quantistica consente alle biglie di "passare attraverso 2 tubi contemporaneamente", ogni marmo quantico vale 2 centesimi. Il valore dei token è additivo:ad esempio, per vincere la partita, Alice può inserire 4 biglie classiche o 2 biglie quantiche, in quanto il valore totale del gettone è in entrambi i casi pari a 4 centesimi", spiega Sebastian Horvat. D'altra parte, Ricordiamo che una particella quantistica non può attraversare più di due località contemporaneamente:ciò si riflette nel fatto che Alice e Bob non possono vincere la partita utilizzando meno di due biglie quantistiche. Quindi, per vincere la partita, il numero di biglie quantistiche inviate da Alice deve essere pari ad almeno la metà del numero totale di coppie di tubi.
Nel loro lavoro, i ricercatori hanno analizzato formulazioni più generali di questo gioco e hanno studiato le prestazioni dei giocatori a seconda del numero di particelle e se le particelle sono classiche, quantistico, o di tipo più generale e ipotetico. Borivoje Dakić aggiunge:"Queste ipotetiche particelle possiedono un maggiore potere di elaborazione delle informazioni, questo è, i loro gettoni corrispondenti valgono più di 2 centesimi. Non è chiaro perché la natura dovrebbe preferire le particelle classiche e quantistiche a queste ipotetiche:questo è qualcosa che dobbiamo ancora studiare in futuro".
Tutto sommato, i giochi di parità forniscono una descrizione alternativa dell'interferenza quantistica all'interno di un quadro più generale e intuitivo, che si spera getterà luce su nuove caratteristiche della sovrapposizione quantistica, analogamente a come è stato approfondito lo studio dell'entanglement quantistico attraverso la formulazione dei cosiddetti "giochi non locali".