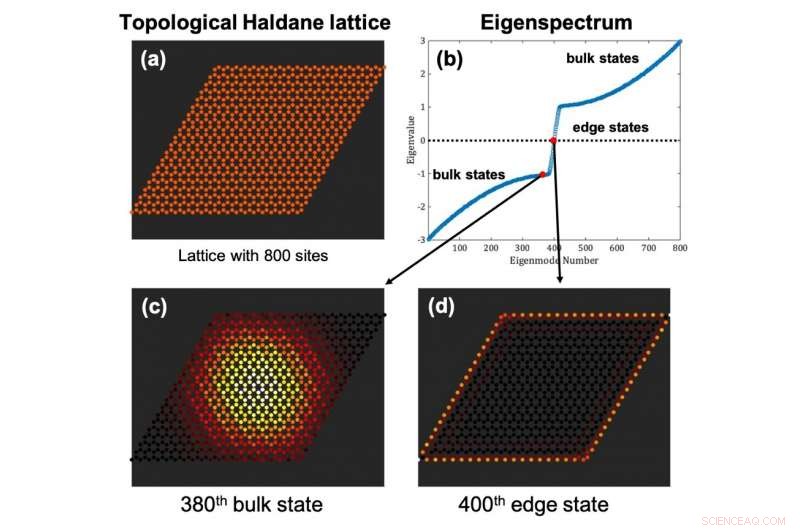
Figura 1:Gli isolanti topologici sono sistemi reticolari di dimensioni finite (a) che mostrano autospettri dove (b) le autoenergie degli stati bulk (c) mostrano un band gap che (d) contiene le autoenergie dei cosiddetti stati edge. Credito:MBI/HU
In uno sforzo congiunto, ricercatori della Humboldt-Universität (Berlino), il Max Born Institute (Berlino) e la University of Central Florida (USA) hanno rivelato le condizioni necessarie per il trasporto robusto di stati entangled di luce a due fotoni in isolanti topologici fotonici, spianando la strada al trasporto di informazioni quantistiche resistente al rumore. I risultati sono apparsi in Comunicazioni sulla natura.
Originariamente scoperto nei sistemi di materia condensata, gli isolanti topologici sono materiali bidimensionali che supportano il trasporto senza scattering (unidirezionale) lungo i loro bordi, anche in presenza di difetti e disordine. In sostanza, Gli isolanti topologici sono sistemi a reticolo finito dove, data un'opportuna terminazione del sottostante reticolo infinito, si formano stati edge che giacciono in un gap energetico ben definito associato agli stati bulk, cioè questi stati limite sono energeticamente separati dagli stati bulk (Fig. 1).
È importante sottolineare che gli stati di bordo a particella singola in tali sistemi sono topologicamente protetti dallo scattering:non possono disperdersi nella massa a causa della loro energia che giace nello spazio vuoto, e non possono disperdersi all'indietro perché gli stati del bordo che si propagano all'indietro sono assenti o non sono accoppiati agli stati del bordo che si propagano in avanti.
La fattibilità di Hamiltoniane complesse ingegneristiche utilizzando reticoli fotonici integrati combinata con la disponibilità di fotoni entangled solleva l'intrigante possibilità di impiegare stati entangled topologicamente protetti nel calcolo quantistico ottico e nell'elaborazione delle informazioni (Science 362, 568, (2018), ottica 6, 955 (2019)).
Raggiungere questo obiettivo, però, è altamente non banale, poiché la protezione topologica non si estende direttamente alla (back)scattering multiparticellare. All'inizio, questo fatto sembra essere controintuitivo perché individualmente, ogni particella è protetta dalla topologia, mentre congiuntamente, le particelle entangled (correlate) diventano altamente suscettibili alle perturbazioni del reticolo ideale. Il principio fisico alla base di questa apparente discrepanza è che, meccanica quantistica, particelle identiche sono descritte da stati che soddisfano un principio di simmetria di scambio.
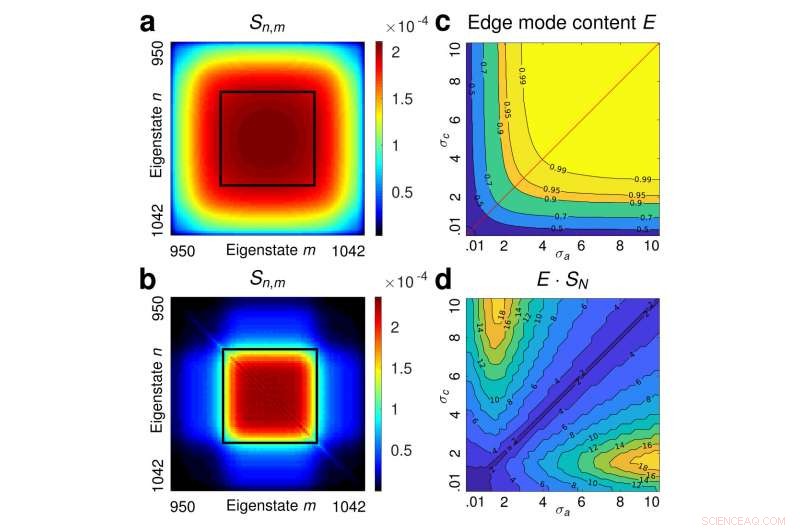
Figura 2:Per identificare la finestra topologica di protezione, i ricercatori hanno considerato uno stato di prodotto spettralmente ampio come stato iniziale e lo hanno propagato attraverso un insieme di 1000 reticoli Haldane casuali. (a) Rappresenta la mappa di correlazione spettrale per lo stato iniziale e in (b) è mostrata la media dell'insieme delle mappe di correlazione spettrale all'interno del sottospazio edge-edge dopo la propagazione attraverso l'insieme di reticoli disordinati. Si trova che le uniche ampiezze a due fotoni che sopravvivono allo scattering indotto dal disturbo si trovano nella regione indicata dal quadrato nero che è la finestra di protezione. Finalmente, (c) e (d) visualizzazione, rispettivamente, il contenuto edge-mode E e il prodotto del contenuto edge-mode con il numero di Schmidt E · SN in funzione delle varianze degli stati iniziali. Credito:MBI/HU
Nel loro lavoro, i ricercatori fanno diversi progressi fondamentali verso la comprensione e il controllo della protezione topologica nel contesto degli stati multiparticellari:
Per essere precisi, esplorano l'impatto del disordine su una gamma di stati a due fotoni che si estendono dai limiti completamente correlati a quelli completamente anti-correlati, coprendo così anche uno stato completamente separabile. Per la loro analisi, considerano due reticoli topologici, uno periodico e uno aperiodico. Nel caso periodico, considerano il modello Haldane, e per il caso aperiodico, un reticolo quadrato, la cui dinamica della singola particella corrisponde all'effetto Hall quantistico, è studiato.
I risultati offrono una chiara tabella di marcia per la generazione di pacchetti d'onda robusti su misura per il particolare disturbo a portata di mano. Nello specifico, stabiliscono limiti alla stabilità degli stati entangled fino a gradi relativamente elevati di entanglement che offrono linee guida pratiche per la generazione di stati entangled utili nei sistemi fotonici topologici. Ulteriore, questi risultati dimostrano che per massimizzare l'entanglement senza sacrificare la protezione topologica, la mappa di correlazione spettrale congiunta degli stati a due fotoni deve rientrare in una finestra topologica di protezione ben definita. (fig.2).