Grafico 1. Catene di spin accoppiate con interazione intrachain di spin più vicino (linea nera continua) e interazione interchain (linea rossa tratteggiata). Credito:Università di Hong Kong
Nel 2013, François Englert e Peter Higgs hanno vinto il Premio Nobel per la Fisica per la scoperta teorica di un meccanismo che contribuisce alla nostra comprensione dell'origine della massa delle particelle subatomiche, che è stato confermato attraverso la scoperta della particella fondamentale prevista dagli esperimenti A Toroid LHC Apparatus (ATLAS) e Compact Muon Solenoid (CMS) presso il Large Hadron Collider dell'Organizzazione europea per la ricerca nucleare (CERN) nel 2012. La modalità Higgs o il meccanismo Anderson-Higgs (dal nome di un altro premio Nobel Philip W Anderson), ha un'influenza diffusa nella nostra attuale comprensione della legge fisica per la massa che va dalla fisica delle particelle, l'elusivo bosone di Higgs "particella di Dio" scoperto nel 2012 ai fenomeni più familiari e importanti dei superconduttori e dei magneti nella fisica della materia condensata e nella ricerca sui materiali quantistici.
La modalità di Higgs, insieme alla modalità Goldstone, è causato dalla rottura spontanea di simmetrie continue nei vari sistemi di materiali quantistici. Però, diverso dalla modalità Goldstone, che è stato ampiamente osservato tramite spettroscopie di diffusione di neutroni e risonanza magnetica nucleare in magneti quantistici o superconduttori, l'osservazione della modalità Higgs nel materiale è molto più impegnativa a causa del suo solito sovrasmorzamento, che è anche la proprietà del suo cugino della fisica delle particelle, l'elusivo bosone di Higgs. Per indebolire questi smorzamenti, due percorsi sono stati suggeriti dal lato teorico, attraverso (1) punti critici quantistici e (2) crossover dimensionale da dimensioni elevate a quelle inferiori. Per (1), persone hanno ottenuto diversi risultati notevoli, mentre ci sono pochi successi in (2).
Per colmare questa lacuna di conoscenza, dal 2020, Signor Chengkang Zhou, poi un primo anno di dottorato. alunno, Dr. Zheng Yan e Dr. Zi Yang Meng della Divisione di Ricerca per la Fisica e l'Astronomia dell'Università di Hong Kong (HKU), progettato un'impostazione di crossover dimensionale tramite catene di spin accoppiate. Hanno applicato la simulazione quantistica Monte Carlo (QMC) per studiare gli spettri di eccitazione del problema. Collaborando con il Dr. Hanqing Wu dell'Università Sun Yat-Sen, Professor Kai Sun dell'Università del Michigan, e il professor Oleg A Starykh dell'Università dello Utah, hanno osservato tre diversi tipi di eccitazione collettiva nel limite quasi-1D, inclusa la modalità Goldstone, la modalità Higgs e la modalità scalare. Combinando analisi numeriche e analitiche, hanno spiegato con successo queste eccitazioni, e in particolare, ha rivelato la chiara presenza della modalità di Higgs nei sistemi magnetici quantistici quasi-1D. Tutti questi risultati possono non solo aiutare a trovare i parametri chiave del modello del materiale, ma rivelano anche un'immagine di come la dimensione sia importante nel materiale condensato. Questi risultati della ricerca sono pubblicati in Lettere di revisione fisica .
Sfondo
I materiali quantistici sono incorporati nella nostra vita quotidiana, come vari componenti elettronici, chip per computer, e pannelli solari. Con il rapido sviluppo della scienza e della tecnologia, la comprensione e la manipolazione delle interazioni quantistiche a molti corpi nei materiali stanno giocando un ruolo sempre più importante. Tale tendenza ha già mostrato il suo primo segno. Per esempio, i materiali 2D quantum moiré, come il grafene a doppio strato ritorto ad angolo magico, hanno attirato molta attenzione e mostrano le loro nuove prestazioni nel realizzare la superconduttività in materiali a base di carbonio invece dei tradizionali materiali a base di silicio. Inoltre, tecnologia informatica quantistica, che si basa sulla teoria della superconduttività e persino sulla topologia si sta rapidamente sviluppando per costruire chip per computer più efficienti oltre la legge di Moore. Insieme a questi sforzi, la ricerca sui magneti quantistici è uno degli oggetti più importanti, in cui il rilevamento della modalità Higgs e delle modalità Goldstone può rivelare i parametri del modello sottostanti del materiale.
Però, poiché l'interazione di miliardi di elettroni deve essere considerata, è difficile indicare direttamente un'immagine chiara di diversi sistemi quantistici a molti corpi tramite la meccanica quantistica. Perciò, metodi numerici, come la simulazione QMC, sono diventate tecnologie utili per studiare i sistemi quantistici a molti corpi. Questi metodi numerici possono fornirci informazioni e proprietà utili dei sistemi quantistici a molti corpi e mostrare il micro meccanismo di questi sistemi. Queste informazioni stimolerebbero lo sviluppo della teoria oltre a guidare il disegno sperimentale, che aiuterebbe gli scienziati e gli ingegneri a scoprire nuovi materiali e componenti quantistici.
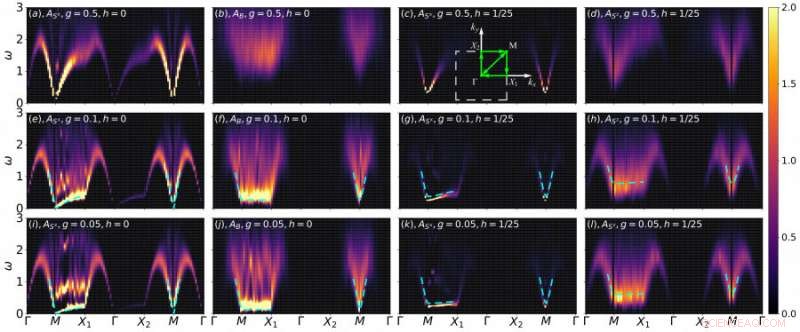
Grafico 2. Gli spettri della modalità Goldstone, la modalità di Higgs, e la modalità scalare cambia con le catene di spin accoppiate che tende a un limite quasi-1D. La prima e la terza colonna sono per la modalità Goldstone. Il secondo indica la modalità scalare mentre il quarto è la modalità Higgs. Credito:Università di Hong Kong
La modalità Higgs tramite crossover dimensionale
Per studiare il micromeccanismo nei sistemi quantistici a molti corpi, i fisici numerici di solito escogitano un modello semplice basato sulla comprensione teorica e sui dati sperimentali. Quindi, applicano metodi di simulazione numerica per studiare il modello nella regione dei parametri ragionevoli. Tale procedura di ricerca è stata utilizzata nello studio del modo di Higgs nei magneti quantistici, tuttavia la sua osservazione è ancora impegnativa a causa della sua consueta caratteristica di sovrasmorzamento. Dal lato della teoria quantistica, gli scienziati hanno suggerito due percorsi. Il primo è attraverso il punto critico quantistico. In questo percorso, ci sono diversi risultati notevoli, compreso il segnale della modalità di Higgs è stato osservato in C 9 h 18 n 2 CuBr 4 . Ma il secondo percorso, che è attraverso il crossover dimensionale verso 1D, è ancora pieno di vuoto e chiede più studio, in parte perché è difficile trovare un sistema quantistico a molti corpi con riduzione dimensionale. Tale riduzione dimensionale indebolisce l'ordine a lungo raggio del sistema e, perciò, inibisce la funzione di sovrasmorzamento della modalità Higgs. Il gruppo di ricerca dell'Università di Hong Kong, l'Università Sun Yat-Sen, l'Università del Michigan e l'Università dello Utah sono riuscite a colmare questi vuoti simulando numericamente un modello di spin quantistico a crossover dimensionale, catene di spin accoppiate (vedi grafico 1).
Il team di ricerca ha ideato un modello di catene di spin accoppiate introducendo l'interazione intercatena. Riducendo la forza di queste interazioni intercatena (cambiando il valore di J⊥ nella Figura 1 verso 0), il modello passerebbe da un sistema 2D a un sistema quasi-1D. Il team di ricerca ha utilizzato il metodo QMC simulando il modello e ha sviluppato un metodo efficace per misurare le funzioni di correlazione di spin e legame. Non solo hanno osservato la modalità di Higgs tramite un crossover dimensionale, ma trovano anche la modalità scalare, che è previsto dalla teoria sine-Gordon. Questi risultati rendono le catene di spin accoppiate un sistema candidato interessante per lo studio della dinamica quantistica collettiva teoricamente e sperimentalmente.
La modalità di Higgs e lo spettro della modalità scalare
Con l'aiuto dei supercomputer Tianhe-II e III, il team di ricerca ha studiato le catene di spin accoppiate nel limite quasi-1D e ha osservato l'evoluzione dello spettro della modalità Goldstone (Figura 2 (g) e (k)), la modalità di Higgs (grafico 2 (h) e (l)), e la modalità scalare (Figura 2 (f) e (j)). La Figura 2 mostra gli spettri ottenuti dalle simulazioni QMC, dove la linea tratteggiata blu rappresenta la relazione di dispersione secondo la combinazione della teoria del campo medio e del modello della teoria di sin-Gordon. Come si può vedere in Figura 2, i risultati numerici si adattano bene alla previsione teorica, il che significa che il team di ricerca è riuscito a catturare il segnale della modalità Higgs. Questi segnali sono molto utili per progettare esperimenti corrispondenti per osservare la modalità di Higgs tramite un crossover dimensionale, come lo scattering di neutroni e la spettroscopia di risonanza magnetica nucleare. Tali risultati entusiasmanti contribuiranno anche alla nostra comprensione della modalità di Higgs nella riduzione dimensionale.
Per descrivere l'emergere della modalità di Higgs e della modalità scalare, il gruppo di ricerca ha anche tracciato la loro dipendenza dalla frequenza (vedi grafico 3), dove g è un fattore che indica quanto è vicino il modello al quasi-1D. Quando g=1, le catene di spin accoppiate sono in un sistema 2D, e con g=0, le catene di spin accoppiate sono in un sistema 1D. Confrontando la dipendenza dalla frequenza dello spettro con diversi g, si può trovare un picco acuto che emerge man mano che g diminuisce, il che significa che i segnali della modalità Higgs e della modalità scalare stanno diventando sempre più forti.
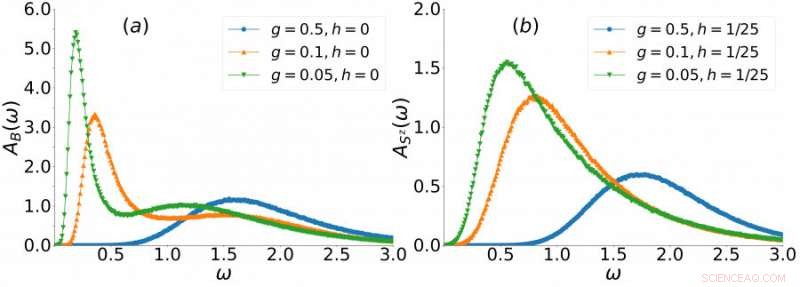
Grafico 3. La dipendenza dalla frequenza dello spettro del modo di Higgs (b) e del modo scalare (a) evolvono con la riduzione della dimensione. In questa riduzione dimensionale, sta emergendo un picco acuto, il che significa che il segnale della modalità scalare e della modalità Higgs diventa più forte. Credito:Università di Hong Kong
Il nuovo fenomeno della fisica tramite crossover dimensionale
Nel quadro della fisica moderna, simmetria e dimensione sono due dei fattori più importanti che determinano le proprietà della fisica quantistica a molti corpi. E il fenomeno causato dalla riduzione delle dimensioni è un argomento chiave nei sistemi magnetici quantistici. La scoperta del gruppo di ricerca ha fornito un modello interessante e un supporto dati, che ci aiutano a capire quale ruolo essenziale gioca la dimensione nel nostro mondo e stimolano lo sviluppo del materiale e dei componenti quantistici di prossima generazione.