I modelli matematici sono stati ampiamente utilizzati per guidare le decisioni del governo sulla pandemia di COVID-19, dalla previsione dei risultati fino alla sperimentazione di potenziali interventi.

Però, la complessità degli scenari del mondo reale pone ancora nuove sfide teoriche per la modellizzazione matematica della diffusione dell'epidemia.

Ad esempio, le prove degli eventi di super-diffusione del COVID-19 indicano che è difficile definire le caratteristiche di questi eventi, che possono variare significativamente nella loro durata e nel numero di persone coinvolte.

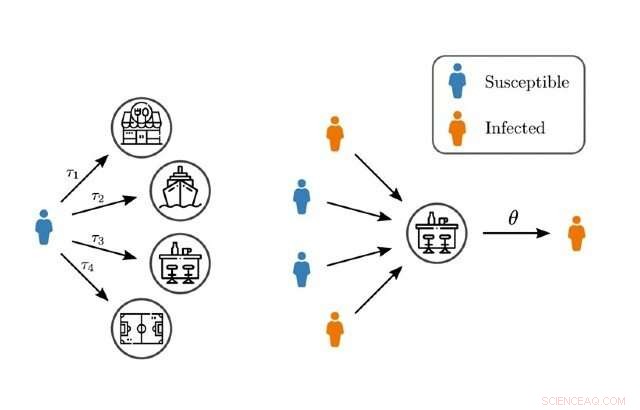
I modelli di rete esistenti di diffusione dell'epidemia spesso si concentrano sui contatti tra coppie di individui mentre si collocano gli individui come sul posto di lavoro, ristoranti, o palestra in genere includono più di due persone. Inoltre, spesso non considerano le durate temporali eterogenee di queste interazioni in un luogo specifico.

In un nuovo studio, pubblicato oggi in Lettere di revisione fisica , i ricercatori hanno sviluppato un nuovo approccio alla modellazione epidemica che considera le interazioni tra due o più persone nella stessa posizione e per periodi di tempo diversi.

Ipotesi sfidanti

Il modello sviluppato dal gruppo di ricerca internazionale, tra cui fisici dell'Università del Vermont e dell'Université Laval, e guidato dalla Professoressa Ginestra Bianconi, un matematico della Queen Mary University di Londra, ha anche preso in considerazione le prove emergenti che suggeriscono che è necessaria una dose infettiva minima perché si verifichi un'infezione.

Questo nuovo approccio di modellazione cambia radicalmente presupposti ben consolidati nella modellazione della rete epidemica, come tassi di infezione lineari con il numero di individui infetti. I risultati mostrano che le co-locazioni combinate con la durata eterogenea dell'esposizione possono portare a tassi di infezione non lineari se è necessaria una dose infettiva minima affinché un'infezione possa verificarsi.

Professoressa Ginestra Bianconi, Professore di Matematica Applicata alla Queen Mary, ha dichiarato:"La co-locazione può coinvolgere gruppi di persone, mentre in genere i modelli di rete di diffusione epidemica si basano su reti di contatto che descrivono interazioni a coppie che possono avere una topologia molto diversa rispetto alle reti di contatto di co-locazione. La co-locazione avviene anche nel tempo, per esempio potrei andare nella stessa palestra di un'altra persona, ma potremmo non incontrarci sempre e potremmo allenarci lì per un periodo di tempo diverso".

"Il nostro approccio abbraccia le eterogeneità delle interazioni dovute alla co-locazione che si verifica tra più di due persone per diversi periodi di tempo e rivela che i nuclei di infezione possono essere non lineari in questi scenari altamente eterogenei, il che significa che se ci sono il doppio degli individui infetti che visitano un dato luogo, la probabilità di infezione può essere anche più del doppio. Questi risultati gettano nuova luce sulla natura molto eterogenea degli eventi di super-diffusione nel contesto di COVID-19".