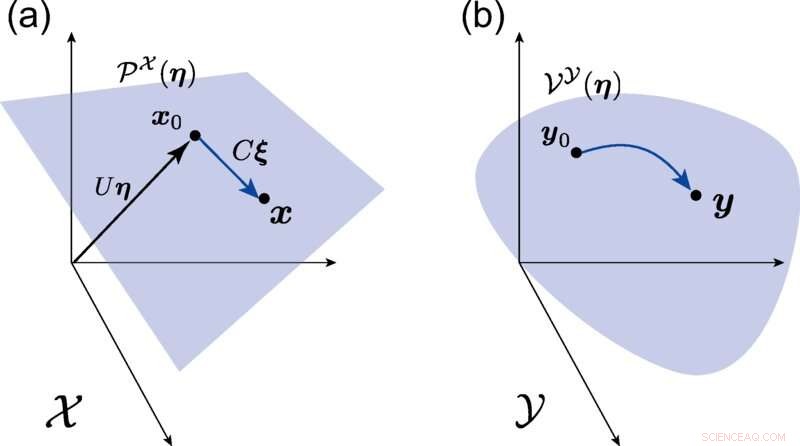
(a) Un sistema di coordinate lineare di X indotta dalla matrice stechiometrica S . Il piano blu rappresenta il sottospazio stechiometrico P X (η). (b) Il collettore stechiometrico V Y (η) (la superficie curva blu) ottenuta mappando P X (η) in Y dalla trasformazione di Legendre ∂φ. Credito:Ricerca di revisione fisica (2022). DOI:10.1103/PhysRevResearch.4.033066
Perdere energia raramente è una buona cosa, ma ora i ricercatori in Giappone hanno mostrato come estendere l'applicabilità della termodinamica a sistemi che non sono in equilibrio. Codificando le relazioni di dissipazione dell'energia in modo geometrico, sono stati in grado di proiettare i vincoli fisici in uno spazio geometrico generalizzato. Questo lavoro può migliorare significativamente la nostra comprensione delle reti di reazione chimica, comprese quelle che sono alla base del metabolismo e della crescita degli organismi viventi.
La termodinamica è la branca della fisica che si occupa dei processi mediante i quali l'energia viene trasferita tra entità. Le sue previsioni sono cruciali sia per la chimica che per la biologia per determinare se determinate reazioni chimiche, o reti di reazioni interconnesse, procederanno spontaneamente. Tuttavia, mentre la termodinamica cerca di stabilire una descrizione generale dei sistemi macroscopici, spesso incontriamo difficoltà nel lavorare sul sistema fuori equilibrio. I tentativi riusciti di estendere il framework a situazioni di non equilibrio sono stati generalmente limitati solo a sistemi e modelli specifici.
In due studi pubblicati di recente in Physical Review Research , i ricercatori dell'Istituto di scienze industriali dell'Università di Tokyo hanno dimostrato che è possibile descrivere complessi processi di reazione chimica non lineare trasformando il problema in una doppia rappresentazione geometrica. "Con la nostra struttura, possiamo estendere le teorie dei sistemi di non equilibrio con funzioni di dissipazione quadratica a casi più generali, che sono importanti per lo studio delle reti di reazioni chimiche", afferma il primo autore Tetsuya J. Kobayashi.
In fisica, la dualità è un concetto centrale. Alcune entità fisiche sono più facili da interpretare se trasformate in una rappresentazione diversa, ma matematicamente equivalente. Ad esempio, un'onda nello spazio temporale può essere trasformata nella sua rappresentazione nello spazio delle frequenze, che è la sua forma duale. Quando si tratta di processi chimici, la forza termodinamica e il flusso sono le rappresentazioni duali non linearmente correlate - il loro prodotto porta alla velocità con cui l'energia viene persa per dissipazione - in uno spazio geometrico indotto dalla dualità, gli scienziati sono stati in grado di mostrare come le relazioni termodinamiche possono essere generalizzato anche in casi di non equilibrio.
"La maggior parte degli studi precedenti sulle reti di reazione chimica si basava su ipotesi sulla cinetica del sistema. Abbiamo mostrato come possono essere gestite più in generale nel caso di non equilibrio impiegando la dualità e la geometria associata", afferma l'ultimo autore Yuki Sughiyama. Possedere una comprensione più universale dei sistemi termodinamici ed estendere l'applicabilità della termodinamica di non equilibrio a più discipline può fornire un punto di vista migliore per analizzare o progettare reti di reazione complesse, come quelle utilizzate negli organismi viventi o nei processi di produzione industriale. + Esplora ulteriormente