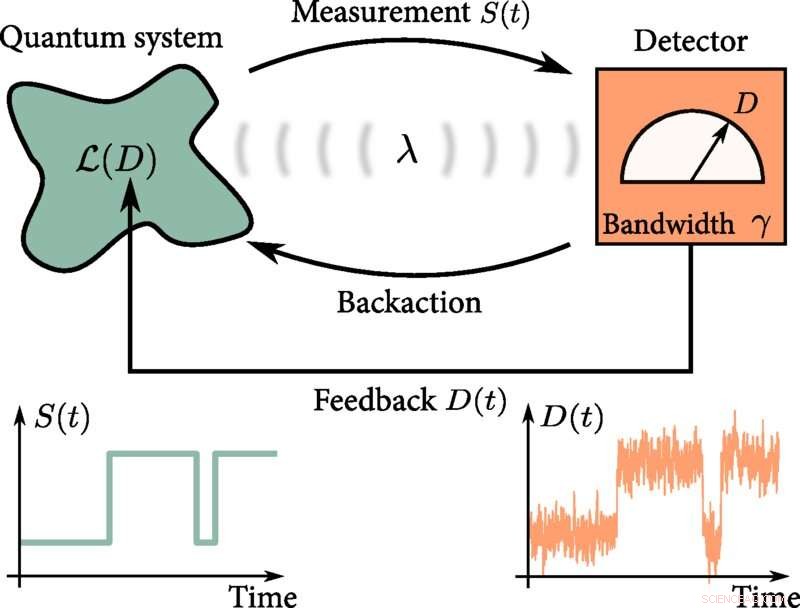
Illustrazione di una configurazione generica di misura e feedback, costituita da un sistema quantistico aperto e un rivelatore con larghezza di banda finita γ. Il rivelatore misura continuamente un sistema arbitrario osservabile. La forza di misura λ determina la controazione di misura. Il feedback continuo viene applicato utilizzando il risultato della misurazione D per controllare il superoperatore Liouville L(D) del sistema. Le tracce temporali visualizzano le traiettorie per lo stato del sistema S(t) e il record di misura D(t) . Credito:Lettere di revisione fisica (2022). DOI:10.1103/PhysRevLett.129.050401
Man mano che le dimensioni della tecnologia moderna si riducono alla scala nanometrica, strani effetti quantistici, come tunneling quantistico, sovrapposizione e entanglement, diventano importanti. Questo apre le porte a una nuova era delle tecnologie quantistiche, in cui è possibile sfruttare gli effetti quantistici. Molte tecnologie quotidiane utilizzano regolarmente il controllo del feedback; un esempio importante è il pacemaker, che deve monitorare il battito cardiaco dell'utente e applicare segnali elettrici per controllarlo, solo quando necessario. Ma i fisici non hanno ancora una comprensione equivalente del controllo del feedback a livello quantistico. Ora, i fisici hanno sviluppato una "equazione principale" che aiuterà gli ingegneri a comprendere il feedback su scala quantistica. I loro risultati sono pubblicati sulla rivista Physical Review Letters .
"È fondamentale studiare come il controllo del feedback può essere utilizzato nelle tecnologie quantistiche al fine di sviluppare metodi efficienti e veloci per il controllo dei sistemi quantistici, in modo che possano essere guidati in tempo reale e con alta precisione", afferma il coautore Björn Annby- Andersson, fisico quantistico all'Università di Lund, in Svezia.
Un esempio di un processo cruciale di controllo del feedback nell'informatica quantistica è la correzione dell'errore quantistico. Un computer quantistico codifica le informazioni sui qubit fisici, che potrebbero essere fotoni di luce o atomi, per esempio. Ma le proprietà quantistiche dei qubit sono fragili, quindi è probabile che le informazioni codificate andranno perse se i qubit sono disturbati da vibrazioni o campi elettromagnetici fluttuanti. Ciò significa che i fisici devono essere in grado di rilevare e correggere tali errori, ad esempio utilizzando il controllo del feedback. Questa correzione degli errori può essere implementata misurando lo stato dei qubit e, se viene rilevata una deviazione da quanto previsto, applicando un feedback per correggerlo.
Ma il controllo del feedback a livello quantistico presenta sfide uniche, proprio a causa della fragilità contro cui i fisici stanno cercando di mitigare. Questa natura delicata significa che anche il processo di feedback stesso potrebbe distruggere il sistema. "È necessario interagire solo debolmente con il sistema misurato, preservando le proprietà che vogliamo sfruttare", afferma Annby-Andersson.
È quindi importante sviluppare una piena comprensione teorica del controllo del feedback quantistico, per stabilirne i limiti fondamentali. Ma la maggior parte dei modelli teorici esistenti del controllo del feedback quantistico richiedono simulazioni al computer, che in genere forniscono risultati quantitativi solo per sistemi specifici. "È difficile trarre conclusioni generali e qualitative", afferma Annby-Andersson. "I pochi modelli in grado di fornire una comprensione qualitativa sono applicabili solo su una classe ristretta di sistemi controllati dal feedback:questo tipo di feedback viene generalmente definito feedback lineare".
'Carta e penna'
Annby-Andersson e i suoi colleghi hanno ora sviluppato un'equazione principale, chiamata "equazione quantistica di Fokker-Planck", che consente ai fisici di tracciare l'evoluzione di qualsiasi sistema quantistico con il controllo del feedback nel tempo. "L'equazione può descrivere scenari che vanno oltre il feedback lineare", afferma Annby-Andersson. "In particolare, l'equazione può essere risolta con carta e penna, piuttosto che dover fare affidamento su simulazioni al computer".
Il team ha testato la propria equazione applicandola a un semplice modello di feedback. Ciò ha confermato che l'equazione fornisce risultati fisicamente sensati e ha anche dimostrato come l'energia può essere raccolta in sistemi microscopici, utilizzando il controllo del feedback. "L'equazione è un punto di partenza promettente per studi futuri su come l'energia può essere manipolata con l'aiuto di informazioni a livello microscopico", afferma Annby-Andersson.
Il team sta ora studiando un sistema che utilizza il feedback per manipolare l'energia in "punti quantici":minuscoli cristalli semiconduttori larghi appena miliardesimi di metro. "Un'importante direzione futura è utilizzare l'equazione come strumento per inventare nuovi protocolli di feedback che possono essere utilizzati per le tecnologie quantistiche", afferma Annby-Andersson. + Esplora ulteriormente