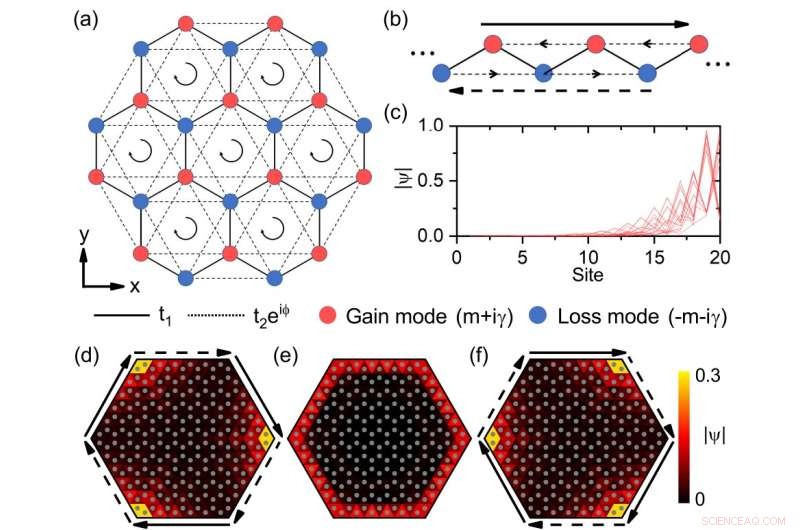
Fig. 1 Modi topologici cutanei ibridi nel modello Haldane non hermitiano. (a) Schema del reticolo non hermitiano. I cerchi rossi (blu) denotano siti con termini di massa sul sito opposti +(m+iγ). (b) Bordo a zigzag del reticolo a nido d'ape come catena 1D, che ha un effetto pelle non hermitiano con guadagno e perdita in loco. La freccia lunga (tratteggiata) indica la corrente di bordo chirale lungo (opposto a) la direzione localizzata [simile in (d) e (f)]. Le frecce nere in (a) e le frecce della linea mediana in (b) indicano le direzioni degli accoppiamenti del prossimo-vicino più vicino t2 e iφ . (c) Profilo di tutti gli automodi per la catena 1D in (b) con 20 siti. Il guadagno e la perdita in loco sono γ=3. (d)-(f) La modalità del bordo chirale per γ=0 (e) diventa modalità skin-topologica per γ=-0,6 (d) e γ=0,6 (f) con diverse direzioni localizzate. Ogni triangolo con un cerchio grigio denota un sito. Qui la modalità del bordo chirale si propaga in senso orario. Credito:Università di Tsinghua
Recentemente, il Professore Associato Yong-Chun Liu del Dipartimento di Fisica e altri hanno scoperto l'effetto topologico cutaneo ibrido indotto da guadagno e perdita e la transizione di fase di parità temporale tra le modalità topologiche cutanee. I risultati della ricerca sono stati pubblicati in Physical Review Letters sotto il titolo "Effetto topologico cutaneo ibrido indotto dalla perdita di guadagno".
I sistemi non hermitiani sono sistemi aperti che possono essere descritti da Hamiltoniani non hermitiani. Ci sono molte nuove proprietà nei sistemi non hermitiani, una delle quali è l'effetto pelle non hermitiano. In questo effetto, tutti gli autostati di un sistema topologico (inclusi gli stati bulk e gli stati edge) sono localizzati su uno dei confini del sistema e la corrispondenza bulk-edge convenzionale viene scomposta. Esistono principalmente due modi per realizzare sistemi non hermitiani:uno utilizza accoppiamenti non reciproci e l'altro utilizza guadagno e perdita.
Nel caso di accoppiamenti non reciproci, la non eremitabilità deriva dalla natura non hermitiana dell'interazione tra diversi siti reticolari. Lo scambio di energia tra i siti del reticolo è asimmetrico, quindi c'è un flusso di energia netto in una direzione e tutta l'energia viene infine raccolta sul confine. Pertanto, i sistemi non reciproci mostrano l'effetto pelle. Nel caso di guadagno-perdita, la non-Ermiticità ha origine dal guadagno e dalla perdita in ciascun sito del reticolo, che equivale ad aggiungere energia immaginaria in loco a ciascun sito del reticolo. Questo tipo di sistema non hermitiano non sempre porta all'effetto pelle. Nei sistemi realistici, gli accoppiamenti non reciproci sono generalmente difficili da ottenere, ma la dissipazione è diffusa e la distribuzione sfalsata della dissipazione equivale a guadagno e perdita. Pertanto, è di grande importanza studiare l'effetto pelle nei sistemi non hermitiani con perdita di guadagno.
Hanno trovato l'effetto pelle-topologico ibrido indotto da guadagno e perdita nei sistemi bidimensionali. Questo tipo di effetto pelle è selettivo, ovvero gli stati bulk e gli stati edge hanno un comportamento diverso. Gli stati di massa non sono influenzati dall'effetto pelle e rimangono estesi, mentre gli stati di bordo mostrano l'effetto pelle e sono ulteriormente localizzati agli angoli. Questo fenomeno ibrido di effetto pelle ed effetto topologico mostra le proprietà uniche dei sistemi topologici non hermitiani, che non hanno analoghi hermitiani o non topologici.
Come esempio specifico, hanno considerato il modello Haldane non hermitiano con guadagno e perdita [Fig. 1(a)]. Nel modello di Haldane, gli stati di bordo topologici sono ottenuti introducendo energia in loco e flusso magnetico locale. È uno dei due modelli importanti per realizzare l'effetto Hall anomalo quantistico nella fisica della materia condensata. Hanno scoperto che se il guadagno e la perdita sfalsati vengono introdotti nei siti più vicini nel modello di Haldane, le modalità dei bordi topologici del sistema mostreranno l'effetto pelle e saranno localizzate agli angoli, mentre le modalità di massa non sono interessate. Quindi, rivela un effetto pelle-topologico ibrido.
Analizzando solo i siti del reticolo ai bordi, questo effetto topologico della pelle di secondo ordine può essere semplificato all'effetto della pelle di primo ordine ai bordi. Nel modello unidimensionale semplificato, ci sono correnti di bordo chirali dovute al flusso magnetico non locale introdotto dai complessi accoppiamenti del vicino più vicino. Sono equivalenti agli accoppiamenti non reciproci, quindi il sistema mostra l'effetto pelle del primo ordine [Fig. 1(b)—(c)]. Al contrario, esiste solo un flusso locale e la non reciprocità si annulla nella maggior parte del sistema. Quindi, le modalità di massa non sono influenzate dall'effetto pelle. Regolando il guadagno e la perdita del sistema, è possibile modificare la direzione delle correnti di bordo, per controllare la direzione dell'effetto topologico cutaneo [Fig. 1 (d)—(f)].
Hanno inoltre ottenuto la relazione tra le simmetrie del tempo di parità (PT) del sistema e l'effetto topologico cutaneo ibrido. Quando si scelgono la condizione al contorno aperta e la condizione al contorno periodica in direzioni diverse, il sistema mostra diversi tipi di simmetrie PT per diversi tipi di spigoli. La simmetria PT globale che mappa qualsiasi modalità localizzata in un confine nell'altro confine preclude l'emergere dell'effetto topologico cutaneo ibrido, mentre la simmetria PT locale con la mappatura all'interno di ciascuna sottocella consente l'esistenza dell'effetto topologico cutaneo ibrido.
Pertanto, l'analisi delle simmetrie PT del sistema fornisce un mezzo semplice ed efficace per giudicare se esiste l'effetto pelle-topologico ibrido. In particolare, hanno scoperto che quando il guadagno e la perdita nel sistema aumentano, si verificherà la transizione di fase PT tra le modalità topologiche della pelle, accompagnata dall'emergere di punti eccezionali (EP). Quando la simmetria PT viene interrotta, le energie proprie dei modi topologici cutanei non sono più reali e le distribuzioni dei modi propri corrispondenti diventano PT-asimmetriche.
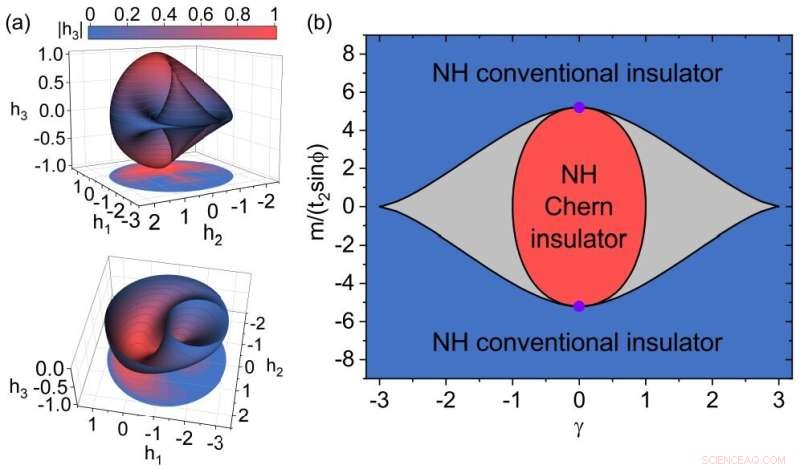
Fig. 2 The topology and phase diagram of the non-Hermitian Haldane model. (a) The surface S mapped from the first Brillouin zone, i.e., mapping from (kx , ky ) to (h1 , h2 , h3 ). The color map represents the magnitude of h3 . The density map below is the projection of the surface. The bottom figure is half of the top figure for h3 <0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points. Credit:Tsinghua University
In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.
The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics. + Esplora ulteriormente