I sistemi quantistici a molti corpi, come i sistemi di bosoni interagenti, sono di fondamentale importanza poiché trovano applicazioni in vari rami della fisica. La propagazione dell'informazione nei sistemi quantistici a molti corpi è governata dal limite di Lieb-Robinson. Ciò quantifica la velocità con cui le informazioni o i cambiamenti si propagano attraverso un sistema quantistico.

Quando si apporta un cambiamento in una parte del sistema, il limite di Lieb-Robinson descrive la velocità con cui questo cambiamento influenza altre parti del sistema. In termini pratici, significa che l'effetto del cambiamento iniziale si diffonderà all'esterno dal suo punto di origine, interessando le regioni vicine del sistema.

Tuttavia, il limite di Lieb-Robinson per i sistemi di bosoni interagenti è rimasto a lungo una sfida.

I ricercatori, guidati dal dottor Tomotaka Kuwahara, team leader del RIKEN Hakubi presso il Centro RIKEN per l'informatica quantistica, affrontano questa sfida nel loro nuovo Nature Communications studiare.

Il dottor Kuwahara ha spiegato l'importanza del loro lavoro a Phys.org, sottolineando l'importanza di comprendere i sistemi quantistici contenenti particelle fondamentali come bosoni e fermioni.

"I sistemi bosonici non hanno, in linea di principio, alcun limite energetico, il che ha reso il legame di Lieb-Robinson nei sistemi bosonici molto impegnativo", ha affermato.

Il limite di Lieb-Robinson

Come accennato in precedenza, il limite di Lieb-Robinson fornisce un limite quantitativo alla velocità con cui le correlazioni o le influenze possono diffondersi tra regioni spazialmente separate di un sistema quantistico.

Ciò significa che la propagazione non può avvenire istantaneamente ovunque ma è invece limitata ad un cono di luce efficace. Ispirato alla teoria della relatività di Einstein, il cono di luce rappresenta tutti i punti dello spazio e del tempo che un segnale luminoso emesso da un evento può raggiungere. Questo crea un doppio cono:uno per il passato e uno per il futuro.

Lo stesso vale per la propagazione dell'informazione nei sistemi quantistici a molti corpi, ovvero sistemi con più di due particelle quantistiche.

"Il confine Lieb-Robinson stabilisce un limite di velocità universale per la velocità con cui le informazioni possono viaggiare in questi sistemi", ha spiegato il dott. Kuwahara.

Secondo il limite di Lieb-Robinson, la propagazione dell'informazione è limitata e decade esponenzialmente con la distanza o con il tempo. Le specificità del decadimento dipendono dal singolo sistema e dalle interazioni che possono verificarsi all'interno del sistema.

Formulato da Elliott Lieb e Derek Robinson nel 1972, il limite di Lieb-Robinson è applicabile solo per i sistemi non relativistici, vale a dire che l'informazione viaggia a velocità molto inferiori a quella della luce.

Il modello Bose-Hubbard

I sistemi di bosoni interagenti sono costituiti da molti bosoni (come i fotoni). Questi sistemi, sebbene comuni, presentano molte sfide, come le interazioni a lungo raggio tra bosoni ed energia illimitata, rendendo difficile lo sviluppo di simulazioni e modelli teorici.

Ma, dalla scoperta del BEC, sono stati sviluppati modelli come il modello di Bose-Hubbard per studiare i sistemi bosonici. Il modello di Bose-Hubbard è un quadro teorico utilizzato per comprendere come si comportano i bosoni quando sono confinati in una struttura reticolare, come gli atomi in un cristallo.

Questo modello tiene conto di due fattori principali. Il primo è il salto dei bosoni da un sito del reticolo all'altro, rappresentato dal parametro hopping. Il secondo è il parametro di interazione sul posto, che rappresenta le forze repulsive tra i bosoni quando occupano lo stesso sito. Questa energia di interazione aumenta man mano che più bosoni occupano lo stesso sito.

Questi fattori incorporano l'interazione tra i bosoni, motivo per cui i ricercatori hanno scelto il modello di Bose-Hubbard per studiare i limiti di Lieb-Robinson nei sistemi di bosoni interagenti.

I limiti superiori

I ricercatori hanno scelto di studiare il legame di Lieb-Robinson per un reticolo D-dimensionale (sistema di bosoni interagenti) governato dal modello di Bose-Hubbard. Hanno trovato tre risultati per questo sistema.

Risultato 1

Questo risultato riguarda l'interazione dei bosoni all'interno del reticolo. I ricercatori hanno scoperto che la velocità del trasporto dei bosoni è limitata, anche nei sistemi con interazioni a lungo raggio. Questa velocità, sebbene limitata, cresce al massimo logaritmicamente con il tempo, che è relativamente lenta.

Questa scoperta fornisce informazioni cruciali sulla dinamica dei sistemi di bosoni, ponendo un limite superiore alla sua velocità.

Risultato 2

Questo risultato si concentra sulla propagazione degli operatori del sistema nel tempo. Gli operatori sono fondamentalmente variabili del sistema, come la quantità di moto. Man mano che questi operatori si propagano, si discostano dall'evoluzione ideale, portando all'accumulo di errori.

Questa propagazione dell'errore determina la velocità con cui le informazioni possono propagarsi nel sistema. Ad esempio, se l'errore è grande, indica che la propagazione delle informazioni è più lenta o più limitata, poiché l'approssimazione si discosta in modo significativo dall'evoluzione ideale del sistema.

Allo stesso modo, se l’errore è piccolo, la propagazione delle informazioni è veloce. Ciò si allinea con il limite di Lieb-Robinson, indicando la presenza di un limite superiore sulla propagazione degli errori.

Nonostante la presenza di un limite superiore alla propagazione degli errori, le interazioni tra bosoni inducono clustering in regioni specifiche. Queste regioni, caratterizzate da concentrazioni più elevate di bosoni, facilitano la propagazione accelerata dell'informazione lungo determinati percorsi o direzioni del reticolo.

Questo fenomeno si allinea con il limite di Lieb-Robinson. Tuttavia, questa accelerazione è limitata e ha una crescita polinomiale che dipende dalla dimensionalità del sistema.

Risultato 3

Questo risultato presenta un modo per simulare questi sistemi utilizzando porte quantistiche elementari (come CNOT). I ricercatori forniscono un limite superiore al numero di porte quantistiche elementari necessarie per simulare in modo efficiente l'evoluzione temporale dei sistemi di bosoni interagenti.

Confronto con sistemi fermionici

I sistemi fermionici mostrano un limite di velocità finito riguardo alla velocità con cui le informazioni possono propagarsi. Prima di questo lavoro, gli scienziati presumevano la stessa cosa per i sistemi bosonici, il che non è vero.

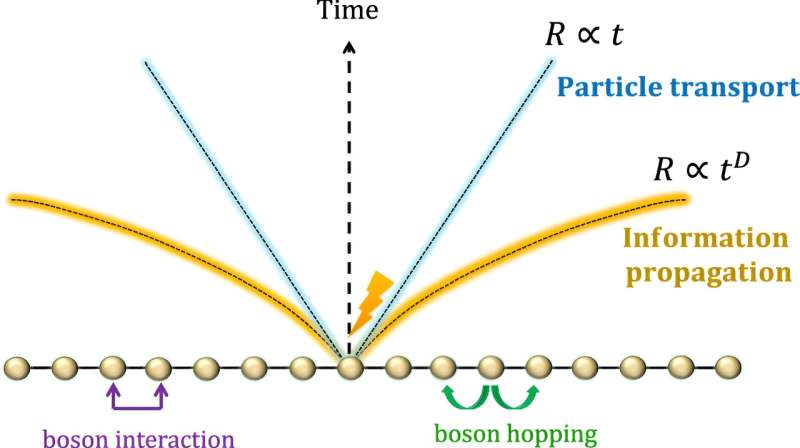
"Il cono di luce si espande molto più velocemente ed è non lineare, cioè accelera nel tempo. Nello specifico, se guardi uno spazio tridimensionale, la distanza che le "informazioni" possono percorrere cresce con il quadrato del tempo. Quindi, in questo senso, i bosoni possono inviare informazioni molto più velocemente dei fermioni, soprattutto col passare del tempo," ha spiegato il dottor Kuwahara.

Ciò dipende dal numero di bosoni che possono occupare lo stesso stato contemporaneamente. In sostanza, più bosoni si uniscono, più velocemente le informazioni possono propagarsi.

"Ma, poiché i bosoni possono muoversi solo a una velocità finita, ci vuole un po' di tempo perché molti di essi si riuniscano, il che porta a una velocità limitata di propagazione dell'informazione. Nel tempo, man mano che più bosoni cooperano, la velocità alla quale si muovono può inviare informazioni aumenta", ha affermato il Dr. Kuwahara.

Questo lavoro apre una nuova finestra sull'esplorazione dei sistemi di bosoni interagenti per la propagazione dell'informazione.

"Prevedo che l'algoritmo verrà utilizzato per simulare la fisica della materia condensata, il che potrebbe portare alla scoperta di nuove fasi quantistiche. Dovrebbe rivelarsi utile anche nella simulazione della termalizzazione quantistica, aiutando ad affrontare la questione fondamentale di come i sistemi quantistici chiusi si stabiliscono in un sistema quantistico." stato stazionario nel tempo", ha concluso il Dott. Kuwahara.