
Quanta sollecitazione subiscono i tubi quando un liquido li attraversa e come dipende dal grado di curvatura del tubo?
Particolarmente cruciali sono le curve dei tubi, ad esempio nell’arco aortico che si collega al ventricolo sinistro del cuore umano. I sistemi di tubazioni negli impianti industriali spesso includono curve di 90 gradi o più, possono essere elicoidali e possono anche avere curve di 180 gradi. I meccanici dei fluidi in Svezia hanno analizzato il flusso dei fluidi in tali tubi con una curvatura di 180 gradi. La loro ricerca è pubblicata sulla rivista Physical Review Fluids .
Le curve dei tubi sono diverse dai loro tratti rettilinei perché, nei tratti curvi, sono presenti forze centrifughe verso l'esterno dovute all'inerzia del liquido all'interno. Questa forza è bilanciata da un gradiente di pressione dalla parete esterna del tubo a quella interna. Poiché le velocità del fluido in un tratto immaginario attraverso il tubo non saranno uguali nella sezione curva – ad esempio, la velocità vicino alla parete esterna del tubo sarà maggiore che vicino alla parete interna – uno schema di flusso secondario, oltre al movimento attraverso il tubo, è installato perpendicolare alla direzione del flusso principale.
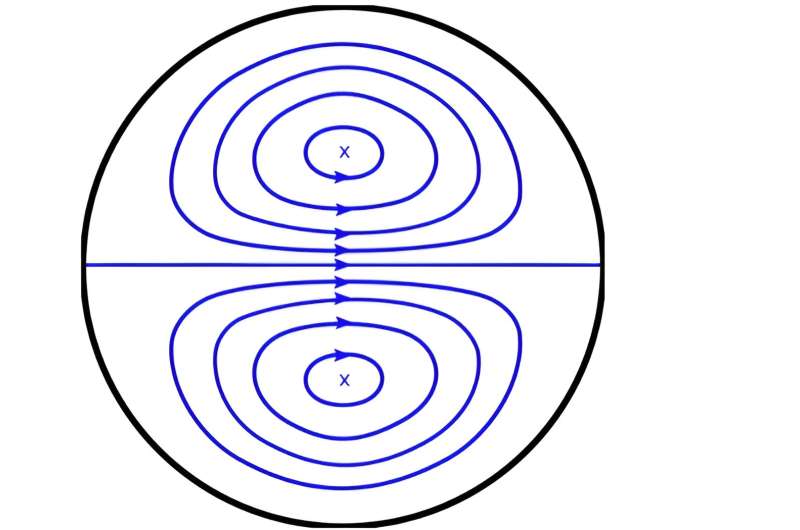
Questo movimento è una coppia di vortici simmetrici e controrotanti, chiamati vortici di Dean, dal nome dello scienziato britannico William Reginald Dean, che compaiono nella prima curva del tubo e possono complicare il flusso successivo, sia per il flusso laminare che per quello turbolento.
Per una singola curva, la geometria interna del flusso può essere descritta dal numero di Dean, che dipende dal raggio del tubo rispetto alla quantità di curvatura nella curva, e dal numero di Reynolds del fluido, che è il rapporto tra le forze inerziali alle forze viscose all'interno di un fluido. I fluidi hanno un numero di Reynolds critico che caratterizza la loro transizione da un flusso laminare regolare a un flusso turbolento, e questo può essere due volte più grande rispetto al flusso rettilineo. (In effetti, il flusso turbolento proveniente da un tubo diritto può tornare ad essere laminare entrando in una sezione a spirale del tubo.)
Approssimativamente, i numeri di Reynolds inferiori a 2.000 indicano un flusso laminare, quelli superiori a 3.500 indicano un flusso turbolento, con una transizione dal flusso laminare a quello turbolento che avviene da qualche parte nel mezzo. Il numero di Dean misura l'intensità del flusso secondario interno.

Daniele Massaro e colleghi del KTH Royal Institute of Technology di Stoccolma hanno utilizzato un metodo raffinato per risolvere numericamente e computazionalmente le famose e complicate equazioni dei fluidi di Navier-Stokes per analizzare la transizione (da flusso laminare a turbolento) in un tubo idealizzato con una curva di 180 gradi, confrontando i loro risultati con i risultati precedenti per tubi a gomito (curvatura di 90 gradi) e toroidali.
Supponendo una curvatura rappresentativa del tubo di 1/3 – il rapporto tra il raggio di una sezione trasversale del tubo e il raggio di curvatura – il gruppo ha diviso il fluido simulato in circa 30 milioni di griglie, non tutte uniformi. Hanno quindi risolto le equazioni per i punti della griglia man mano che cambiavano nel tempo.
Eseguendo un'analisi di stabilità, determinando la crescita di imperfezioni minuscole e infinitesimali che compaiono nel fluido liscio iniziale, il calcolo determina i cambiamenti nel fluido mentre segue la curva. Le variazioni avvengono attraverso tutte le sezioni trasversali verticali del fluido e lungo la lunghezza del tubo. In questo modo si può determinare la transizione del flusso da laminare a turbolento.
L’intenso calcolo – per il quale erano necessari supercomputer, ha detto Massaro, con operazioni che potevano richiedere mesi – ha rilevato che il numero di Reynolds critico per la transizione è 2.528. Questa è la regione del numero di Reynolds del fluido, indipendentemente dal tipo, dove si verifica l'instabilità e la forma della struttura porta alla transizione alla turbolenza. Questo punto di transizione è noto anche come "biforcazione di Hopf". L'instabilità per la curva a 180 gradi si sviluppa in modo molto simile a quella di una curva a 90 gradi. Il numero di Reynolds critico per una curva di 90 gradi è 2.531, mentre per un toro è 3.290.
A causa della natura dettagliata dell'instabilità, si prevede che i tubi con curve superiori a 180 gradi siano simili, fino a un certo punto. Per tubi con curve più corte, la biforcazione di Hopf deve scomparire quando l'angolo di curvatura si avvicina allo zero con il flusso che rimane laminare. Il gruppo stima che la biforcazione svanisca con una curva di circa 20 gradi.
Sebbene la ricerca abbia evidenti applicazioni industriali, l’estensione al cuore non è semplice a causa della differenza tra il sangue reale e il flusso idealizzato di questo studio. "Il nostro studio aiuta a capire dove potrebbe verificarsi una transizione improvvisa nell'arco aortico laminare", ha affermato Massaro, coautore dello studio e studente laureato presso il dipartimento di Ingegneria Meccanica del KTH Royal Institute of Technology di Stoccolma. . "In effetti, il regime turbolento dell'aorta può essere potenzialmente correlato a varie malattie cardiache."
Ulteriori informazioni: Daniele Massaro et al, Stabilità globale del flusso del tubo con curvatura a 180∘ con adattività della mesh, Fluidi per revisione fisica (2023). DOI:10.1103/PhysRevFluids.8.113903
Informazioni sul giornale: Fluidi per revisione fisica
© 2023 Rete Scienza X