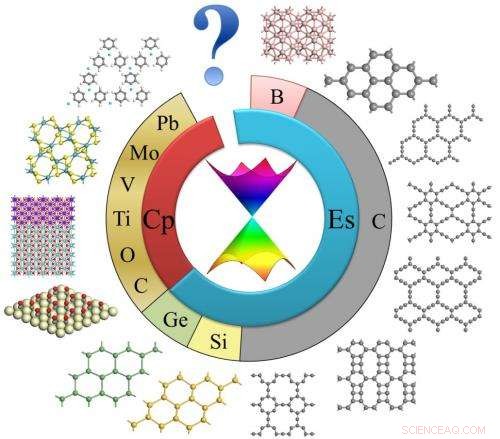
Schema di materiali 2-D con coni di Dirac. Credito:©Science China Press
Grafene, un foglio a nido d'ape bidimensionale (2D) composto da atomi di carbonio, ha attratto intensi interessi in tutto il mondo per le sue eccezionali proprietà e le promettenti prospettive sia nella scienza di base che in quella applicata. Il grande sviluppo del grafene è strettamente correlato alla struttura elettronica unica, questo è, Coni Dirac. Il cono che rappresenta la dispersione lineare dell'energia a livello di Fermi fornisce fermioni privi di massa al grafene, portando a vari effetti Hall quantistici, mobilità ultra elevata dei portatori, e molti altri nuovi fenomeni e proprietà.
Il cono di Dirac è speciale ma potrebbe non essere esclusivo del grafene. Recentemente, si prevede che sempre più materiali 2D posseggano coni di Dirac, come silicene e germanene (silicio simile al grafene e germanio, rispettivamente), diversi grafini (allotropi del carbonio sp-sp2), e così via. Ma questi sistemi Dirac 2D sono così rari rispetto ai numerosi materiali 2D. Sono necessarie una profonda conoscenza di tutti i sistemi Dirac 2D conosciuti e una strategia per cercarne di nuovi.
Un nuovo articolo pubblicato su Rassegna scientifica nazionale ha presentato i recenti progressi sugli studi teorici di vari materiali Dirac 2D.
In questo documento, le proprietà strutturali ed elettroniche del grafene, silicio, germanene, grafia, diversi allotropi di boro e carbonio, ossidi di metalli di transizione, cristalli organici e organometallici, quadrato MoS2, e sono stati riassunti i reticoli artificiali (gas elettronici e atomi ultrafreddi). Come ha affermato l'autore, "la maggior parte dei materiali Dirac ha simmetria di inversione spaziale", "Molti di loro sono bipartiti e composti da un solo elemento", e "la struttura a nido d'ape esagonale è comune nei materiali Dirac atomici". Poiché "la struttura del cono di Dirac fornisce fermioni privi di massa al grafene, che porta a effetti Hall quantistici semi-interi/frattali/frattali, mobilità ultraelevata dei portatori", si prevedeva che altri sistemi Dirac 2D avessero proprietà simili, e alcuni possiedono persino una nuova fisica oltre il grafene.
Sulla base delle discussioni di cui sopra, gli autori hanno ulteriormente studiato come i punti di Dirac si muovono e si fondono in questi sistemi. Hanno detto che la deformazione può spostare il punto di Dirac in una nuova posizione k (reciproca). Ma "quando due punti di Dirac con fasi di Berry opposte si muovono nello spazio k sotto qualsiasi perturbazione e arrivano allo stesso punto, si fondono e le loro fasi Bacca si annientano a vicenda". Inoltre, il teorema di von Neumann-Wigner è stato applicato per spiegare la scarsità di sistemi di Dirac 2D. Quindi sono stati dedotti i requisiti rigorosi per un sistema 2D per ottenere i coni Dirac, che è legato alla simmetria, parametri, livello di Fermi, e sovrapposizione di banda.
Questo articolo ha osservato che "i coni di Dirac non sono solo la dispersione lineare dell'energia attorno a punti discreti, ma anche le singolarità nello spettro delle Hamiltoniane e sono topologicamente protetti". Gli autori hanno sottolineato "Guardando al futuro, crediamo che verranno scoperti sempre più materiali 2D Dirac, e una conoscenza approfondita delle condizioni esistenti dei coni Dirac è di grande aiuto nella ricerca/progettazione di nuovi sistemi."