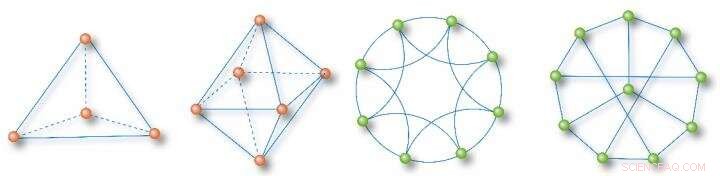
Esempi di reti totalmente omogenee:un tetraedro, una rete minima a 2 cavità, una rete più vicina a 8 nodi, e una rete ottimale per la sincronizzazione a 10 nodi Credito:Science China Press
Dall'inizio del secolo scorso, la ricerca sui sistemi complessi ha fatto avanzare i campi del caos, frattali e reti. Una rete è composta da nodi e archi, dove i nodi rappresentano gli elementi di un sistema complesso e gli archi descrivono le interazioni tra di essi. Tali relazioni nodo-bordo possono essere rappresentate da una matrice di adiacenza, il cui ordine è uguale al numero di nodi e ogni somma di righe corrisponde a un grado di nodo. L'eterogeneità dei gradi dei nodi porta all'emergere di strutture a forma di stella centrate sui nodi hub.
Per affrontare l'eterogeneità dei gradi del nodo, è entrato in gioco il modello di rete scale-free, attirando un'ampia attenzione. Ad oggi, man mano che la tecnologia di Internet avanza e la ricerca sulla rete procede, i ricercatori si sono resi conto che la percezione tradizionale delle reti eterogenee basate su stelle è insufficiente per descrivere reti complesse in evoluzione e problemi scientifici di rete. Ad esempio, ci sono molte comunità online su Internet che dipendono da strutture sociali basate sul ciclo per la comunicazione di gruppo e la diffusione delle informazioni.
Il funzionamento della rete e le proprietà dinamiche hanno connessioni sempre più strette con caratteristiche topologiche di rete di ordine superiore, sottostrutture omogenee e invarianti topologici. Così, spostare l'attenzione dai gradi dei nodi ai numeri dei cicli rivela molte sottoreti totalmente omogenee in reti complesse. Qui, una rete totalmente omogenea è definita come una rete con nodi aventi lo stesso grado, stessa circonferenza (numero di spigoli nel ciclo più piccolo di un nodo), e stesso percorso-sum (somma dei percorsi più brevi a un nodo da tutti gli altri nodi). Alcuni esempi tipici sono mostrati nella Figura 1 a scopo illustrativo.
Alla fine del XIX secolo, Poincaré scoprì che i confini sono fondamentali per differenziare forme geometriche come dischi, sfere e tori. Ha scomposto un oggetto geometrico in componenti di base chiamati simplessi (punto, linea, triangolo, tetraedro, eccetera.), e poi ha introdotto i concetti di raggruppamento per omologia, Numero di Betti e matrice di correlazione nodo-bordo, e la formula di Eulero-Poincaré, che mostra che la somma alternativa dei simplessi è uguale alla somma alternativa dei numeri di Betti.
L'idea di base di Poincaré è quella di dividere una forma geometrica complessa in modo da semplificare la procedura per una soluzione. È stato in grado di farlo perché ci sono molte sottoreti totalmente omogenee, come triangoli e tetraedri (denominati cricche nella teoria dei grafi o simplessi in topologia) in una rete complessa. Sono strutture di base per supportare le funzioni di rete, diverse dalle stelle, sono cicli. Con questi elementi di base, è possibile descrivere una rete utilizzando una serie di spazi vettoriali sul campo binario.
Per esempio, lo spazio vettoriale ha come base gli spigoli, con dimensione pari al numero di spigoli; lo spazio vettoriale ha come base i triangoli, con dimensione pari al numero di triangoli, e così via. Poiché il confine di un triangolo è costituito da bordi, i due spazi vettoriali adiacenti e possono essere correlati tramite un operatore di confine, e la sua matrice di confine può essere utilizzata per la presentazione e l'analisi. La matrice di confine ha un contenuto matematico più ricco ed è più utile della matrice di adiacenza. Ad esempio, usando il rango della matrice di confine si può calcolare il numero di Betti, un'importante invariante della rete, che è il numero di cavità linearmente indipendenti di diversi ordini nella rete, stabilire un gruppo di omologia. La Figura 2 mostra le relazioni di alcuni spazi vettoriali e dei corrispondenti operatori di confine.
Nel 2002, Xiaofan Wang e Guanrong Chen hanno pubblicato il primo criterio di sincronizzazione della rete. È stato seguito da una serie di lavori tra cui l'introduzione di reti totalmente omogenee tramite l'ottimizzazione di Dinghua Shi, Guanrong Chen e Xiaoyong Yan nel 2013, rivelando che la rete totalmente omogenea con una circonferenza più lunga e una somma dei percorsi più corta ha una migliore sincronizzazione tra reti della stessa dimensione. Inoltre, nel 2006, Linyuan Lü e Tao Zhou hanno usato l'operatore H per scoprire la relazione tra grado del nodo, Indice H e valore del kernel, stabilire il teorema DHC. Nello studio dell'indice di ciclo, un lavoro importante è lo studio empirico di Bassett et al. nel 2018 sulla rete funzionale cerebrale, in cui hanno sottolineato l'importanza delle cricche e delle cavità nel funzionamento della rete. Ultimo, ma non per importanza, abbiamo recentemente scoperto la stretta relazione tra i numeri caratteristici di Eulero e la sincronizzabilità della rete.
Questa serie di importanti risultati progressivi dimostra il significato e l'importanza della ricerca interdisciplinare in fisica, biologia e matematica. Considerando che questa nuova direzione dell'analisi strutturale di rete utilizzando strumenti topologici algebrici è promettente, i ricercatori hanno scelto di pubblicare il loro articolo attuale, "Reti totalmente omogenee, " in Rassegna scientifica nazionale .
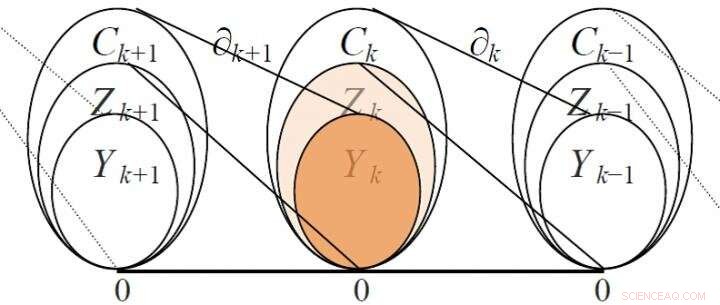
Relazioni di alcuni spazi vettoriali e dei loro corrispondenti operatori al contorno (Zk è un gruppo di cicli, Yk è un gruppo di confine) Credito:Science China Press