Se hai mai provato a districare un paio di auricolari, capirai come anelli e cavi possono essere attorcigliati. Il DNA può aggrovigliarsi allo stesso modo, e in alcuni casi, deve essere tagliato e ricollegato per risolvere i nodi. Ora un team di matematici, biologi e scienziati informatici hanno svelato come i batteri di E. coli possono scollegare il DNA aggrovigliato mediante un processo di riconnessione locale. La matematica dietro la ricerca, recentemente pubblicato in Rapporti scientifici , potrebbe avere implicazioni ben oltre la biologia.

I batteri E. coli possono causare malattie intestinali, ma sono anche cavalli da lavoro di laboratorio. Il genoma di E. coli è un singolo cerchio di DNA a doppia elica. Prima che una cellula di E. coli si divida, quel cerchio viene copiato. Aprendo la doppia elica per copiarla si generano tensioni di torsione altrove lungo la molecola, proprio come srotolare un cavo in un punto lo farà avvolgere eccessivamente in un altro. Il processo si traduce in due anelli attorcigliati di DNA che si incrociano come un trucco degli "anelli magici".

Per separare gli anelli, E. coli utilizza un enzima chiamato topoisomerasi IV, che taglia con precisione un segmento di DNA, consente ai loop di passare attraverso l'interruzione e quindi risigilla l'interruzione. Poiché la topoisomerasi IV è così importante per i batteri, è un bersaglio allettante per antibiotici come la ciprofloxacina. Ma quando la topoisomerasi IV è assente, un altro complesso enzimatico può intervenire per effettuare questo scollegamento, anche se meno efficiente. Questo complesso introduce due interruzioni e scollegamenti ricollegando le quattro estremità libere.

"Ci sono altri modi per scollegare gli anelli, ma come fanno?" disse Mariel Vazquez, professore di matematica e di microbiologia e genetica molecolare all'Università della California, Davis.

Un percorso, Vazquez ha detto, è che gli enzimi di riconnessione rimuovono un collegamento alla volta fino ad arrivare a zero. Questa soluzione è stata favorita dai biologi.

Ma i matematici considerano il problema in modo leggermente diverso. Capiscono il DNA come una curva flessibile nello spazio tridimensionale. Alcuni punti della curva possono essere spezzati e ricollegati. A un matematico, ci sono molti potenziali percorsi per far funzionare i processi di riconnessione, inclusi alcuni in cui il numero di collegamenti aumenta effettivamente prima di tornare indietro.

"Questi sono tutti uguali per un matematico, ma non a un biologo, " ha detto Vazquez. Per determinare il percorso più probabile e risolvere il problema, si sono rivolti alla modellazione computazionale.

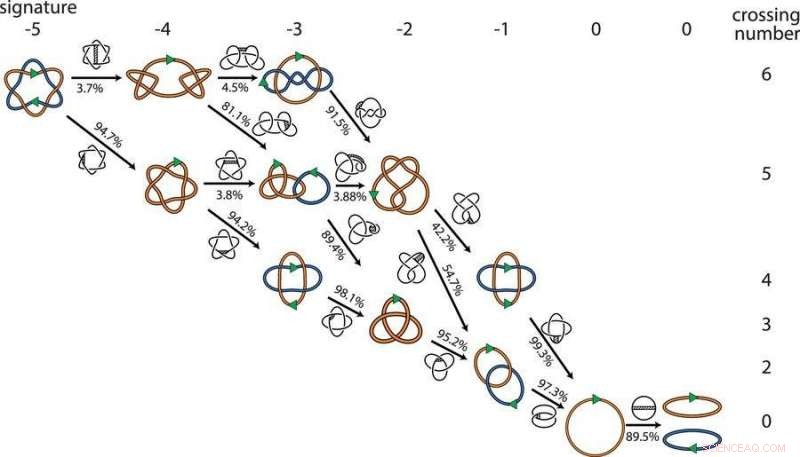
Vazquez e colleghi hanno sviluppato un software per computer con il DNA rappresentato come catene flessibili per modellare le possibili posizioni in cui gli enzimi di riconnessione potrebbero tagliare e ricollegare le catene. Globale, hanno modellato milioni di configurazioni che rappresentano 881 diverse topologie, o forme matematiche, e identificato centinaia di percorsi minimi per ottenere due cerchi di DNA collegati in un massimo di nove punti fino a due cerchi separati.

Il modello al computer ha confermato l'intuizione dei biologi:annullare un collegamento alla volta è il percorso preferito per separare i cerchi del DNA.

I risultati potrebbero avere implicazioni ben oltre la biologia del DNA, ha detto Vazquez. Ci sono altri esempi in natura di oggetti che si scontrano, rompere e riconnettersi, come la dinamica dei vortici fluidi collegati, o gli schemi formati da anelli di fumo, Per esempio. Quando i brillamenti solari vengono espulsi dal sole, potenti linee di campo magnetico si incrociano e si riconnettono.

"La matematica non è specifica del DNA, e il calcolo può essere adattato, " Ha detto Vazquez.