
Questa animazione mostra l'evoluzione della deformazione della forma, risultante dall'applicazione dell'algoritmo al set di dati del drago. Per quanto riguarda il set di dati armadillo, la forma rossa prima dell'ottimizzazione è stata creata dalla deformazione non lineare della forma blu. Entrambi i set di punti sono composti da 437, 645 punti ciascuno. Credito:Università di Kanazawa
Un problema di registrazione dell'insieme di punti è un'attività che utilizza due forme, ciascuno costituito da un insieme di punti, stimare la relazione dei singoli punti tra le due forme. Qui, una "forma" è come un corpo o un viso umano, che è simile a un altro corpo o viso ma mostra diversità morfologica. Prendendo come esempio il viso:la posizione centrale della pupilla di un occhio varia a seconda degli individui ma si può pensare che abbia una corrispondenza con quella di un'altra persona. Tale corrispondenza può essere stimata deformando gradualmente una forma per essere sovrapponibile all'altra. La stima della corrispondenza di un punto su una forma ad un punto su un'altra è il problema di registrazione dell'insieme di punti. Poiché il numero di punti di una forma potrebbe essere milioni, la stima della corrispondenza è calcolata da un computer. Ciò nonostante, fino ad ora, anche quando è stato utilizzato il metodo convenzionale più veloce, ci è voluto molto tempo per il calcolo per la registrazione di ca. 100, 000 punti. Così, sono stati ricercati algoritmi che potrebbero trovare una soluzione molto più velocemente senza compromettere la precisione. Per di più, la registrazione preliminare prima della stima automatizzata era un prerequisito per il metodo di calcolo convenzionale, quindi sono desiderabili algoritmi che non necessitano di registrazione preliminare.
Prof. Osamu Hirose, un giovane scienziato dell'Università di Kanazawa, ha lavorato su questo problema. Nel suo studio, è stato adottato un approccio completamente nuovo; un problema di registrazione di insiemi di punti è definito come massimizzazione della probabilità a posteriori 1) nella statistica bayesiana 2) e l'uniformità di un campo di spostamento 3) è definita come probabilità a priori 4). Di conseguenza, è stato scoperto un nuovo algoritmo in grado di trovare una soluzione ad un tipico problema di registrazione di insiemi di punti anche senza una sufficiente registrazione preliminare. Inoltre, sostituendo alcuni calcoli di questo algoritmo con l'approssimazione, i problemi di registrazione del set di punti possono essere risolti drasticamente più velocemente rispetto ai metodi convenzionali. Per esempio, per due set di punti composti da ca. 100, 000 punti ciascuno, l'applicazione del presente metodo ha avuto successo nel completare una registrazione altamente accurata entro 2 minuti, mentre il metodo più veloce pubblicamente disponibile impiegava circa tre ore. Anche, come mostrato nell'illustrazione, il metodo proposto ha registrato con successo il set di dati "drago", dove entrambi i set di punti erano composti da 437, 645 punti ciascuno. Il tempo di calcolo è stato di circa 20 min. Sebbene il presente calcolo ad alta velocità utilizzi approssimazioni, l'esattezza della registrazione non è ridotta in misura percettibile, come dimostrato da esperimenti numerici.
Utilizzando l'algoritmo, nuovi personaggi CG possono essere creati automaticamente, e con ciò, può essere una tecnica che fa risparmiare lavoro per i progettisti di computer grafica. La seconda illustrazione mostra un esempio di applicazione dell'algoritmo. La forma di origine (a) e la forma di destinazione (b) sono state ottenute da un database pubblico e utilizzate come input dell'algoritmo. La forma (c) è il risultato della prima registrazione, mostrando che la forma di origine è diventata simile alla forma di destinazione con le caratteristiche della forma di origine mantenute. La forma (d) è il risultato della seconda registrazione, che mostra la forma di origine da deformare più vicino alla forma di destinazione.
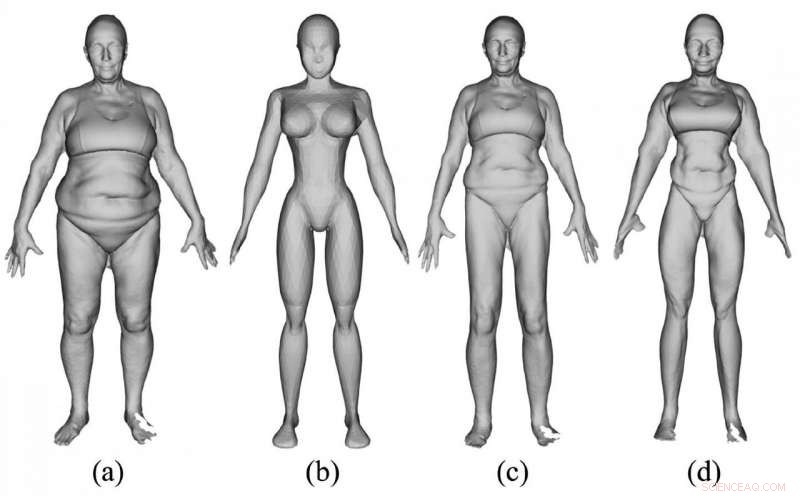
(a) Forma della sorgente. (b) Forma del bersaglio della registrazione dell'insieme di punti. (c) Forma dopo la prima registrazione. (d) Forma dopo la seconda registrazione. Credito:Università di Kanazawa

La forma rossa è costituita da una deformazione non rigida della forma blu; le due forme non sono sovrapponibili tra loro mediante rotazione delle forme. La forma più a sinistra rappresenta il posizionamento iniziale, dimostrando che la registrazione preliminare del set di punti non è stata eseguita prima della registrazione automatizzata. Il processo di ottimizzazione è mostrato da sinistra a destra. Credito:Università di Kanazawa
L'importanza dei problemi di registrazione del set di punti è dovuta alla loro vasta gamma di applicazioni nei campi della computer grafica (CG) e della computer vision. L'autenticazione personale tramite riconoscimento facciale utilizzata sugli smartphone può essere interpretata come un'applicazione di registrazione del set di punti. Ulteriore, fondendo la forma tridimensionale di alcune due persone, chiamato "morphing, " può essere eseguita tramite la registrazione del set di punti. Inoltre, esiste uno studio ben noto che ha consentito il restauro di un modello facciale tridimensionale della defunta Audrey Hepburn da una singola immagine, che utilizzava una tecnica che può essere interpretata come registrazione dell'insieme di punti. Perciò, poiché le registrazioni dei set di punti con un'ampia varietà di applicazioni possono ora essere eseguite a una velocità molto elevata con un'elevata precisione, si prevede che il metodo stabilito in questo studio sarà utilizzato come tecnologia di base in questo campo di ricerca.
D'altra parte, il metodo potrebbe essere ulteriormente migliorato. Sebbene sia notevolmente più veloce del metodo convenzionale, la velocità di calcolo può diventare un problema quando il numero di punti in un insieme di punti raggiunge milioni. Il prof. Hirose sta ulteriormente sviluppando metodi per consentire il calcolo di un problema di registrazione di set di punti così grande in pochi minuti. I risultati preliminari mostrano una grande promessa per ulteriori sviluppi di successo.