Reti o grafici sono descrizioni matematiche della struttura interna tra i componenti di un sistema complesso, come le connessioni tra i neuroni, interazioni tra proteine, contatti tra individui in mezzo alla folla, e le interazioni tra gli utenti nelle piattaforme social online. I collegamenti nella maggior parte delle reti reali cambiano nel tempo, e tali reti sono spesso chiamate reti temporali. La temporalità dei collegamenti codifica l'ordine e la causalità delle interazioni tra i nodi e ha un profondo effetto sulla funzione della rete neurale, propagazione di malattie, aggregazione e raccomandazione delle informazioni, comparsa di comportamenti cooperativi, e controllabilità della rete. La crescente ricerca si è concentrata sull'estrazione dei modelli in una rete temporale e sulla previsione della sua evoluzione futura utilizzando tecniche di apprendimento automatico, in particolare le reti neurali a grafo. Però, come quantificare il limite di prevedibilità di una rete temporale, ovvero il limite che nessun algoritmo può superare, è ancora una questione aperta.

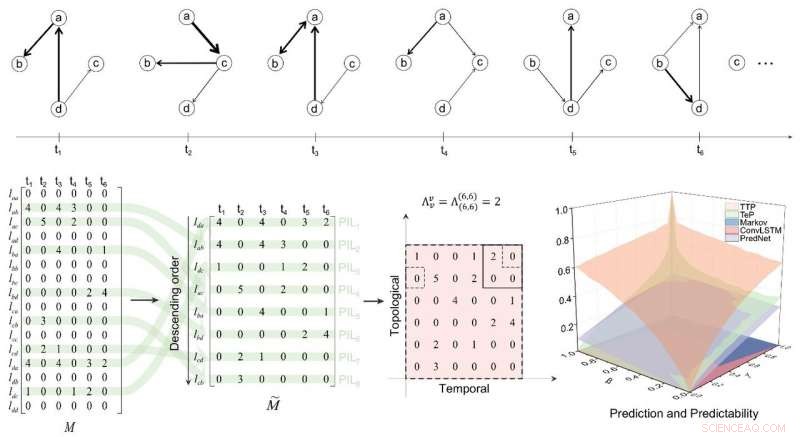
Recentemente, un gruppo di ricerca guidato da Xianbin Cao con la Beihang University, Pechino, e Gang Yan alla Tongji University, Shanghai, ha pubblicato un documento intitolato "Prevedibilità delle reti temporali reali" in Rassegna scientifica nazionale e ha proposto un quadro per quantificare la prevedibilità delle reti temporali in base al tasso di entropia dei campi casuali.

Gli autori hanno mappato ogni data rete su una matrice temporalità-topologia, e poi ha esteso il classico calcolo del tasso di entropia (che è applicabile solo alle matrici quadrate) a matrici arbitrarie tramite operatori di regressione. I vantaggi significativi di questa prevedibilità topologica temporale sono stati convalidati in due modelli tipici di reti temporali. Applicando il metodo per calcolare la prevedibilità di 18 reti reali, gli autori hanno scoperto che in diversi tipi di reti reali, i contributi della topologia e della temporalità alla prevedibilità della rete sono significativamente variabili; Sebbene la linea di base teorica e la difficoltà della prevedibilità topologica temporale siano molto più elevate di quelle delle serie temporali unidimensionali, le prevedibilità topologico-temporali della maggior parte delle reti reali sono ancora superiori a quelle delle serie temporali.

Il limite di prevedibilità calcolato in questa ricerca è una proprietà intrinseca delle reti temporali, cioè è indipendente da qualsiasi algoritmo predittivo, quindi può essere utilizzato anche per misurare il possibile spazio di miglioramento degli algoritmi predittivi. Gli autori hanno esaminato tre algoritmi predittivi ampiamente utilizzati e hanno scoperto che le prestazioni di questi algoritmi sono significativamente inferiori ai limiti predittivi nella maggior parte delle reti reali, suggerendo la necessità di nuovi algoritmi predittivi che tengano conto sia delle caratteristiche temporali che topologiche delle reti.